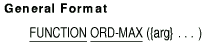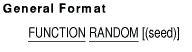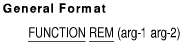Compaq COBOL
Reference Manual
7.31 ORD
Description
The ORD function returns an integer value that is the ordinal position
of the argument in the collating sequence for the program. The lowest
ordinal position is 1.

arg
is an alphabetic or alphanumeric argument one character in length.
Rules
- The type of this function is integer.
- The value returned is the ordinal position of the specified
character in the program collating sequence. (See the information on
the ALPHABET clause in Chapter 4.)
Example
COMPUTE POSITION = FUNCTION ORD (SINGLE-CHAR).
|
If SINGLE-CHAR (an alphabetic or alphanumeric data item) has the value
"A", the integer representing the ordinal position of "A" in the
program collating sequence (66 for native) is the value returned and
stored in POSITION (a numeric integer data item). (The numeric
representation of a character is not the same as its ordinal position.
Numeric representation starts at 0, whereas ordinals start at 1. Thus,
the ordinal value of a character is always 1 greater than its numeric
value.)
7.32 ORD-MAX
Description
The ORD-MAX function returns a value that is the ordinal number of the
argument that contains the maximum value.
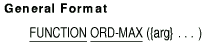
arg
is an alphabetic, alphanumeric, integer, or numeric argument.
Rules
- The type of this function is integer.
- The arguments must be all alphabetic, all alphanumeric, all
integer, or all numeric, except that integer and numeric arguments can
be mixed and alphabetic and alphanumeric arguments can be mixed.
- The returned value is the ordinal number that corresponds to the
position of the argument having the greatest value in the argument
series.
- The comparisons used to determine the greatest value are made
according to the rules for simple conditions. (See Chapter 6.)
- If more than one argument has the same greatest value, the number
returned corresponds to the position of the leftmost argument having
that value.
- If there is only one argument, the value returned is 1.
Example
COMPUTE RSULT = FUNCTION ORD-MAX (A, B, C).
|
A, B, and C are alphanumeric data items one character in length. If the
value "A" is in A, "B" is in B, and "C" is in C, the value returned and
stored in RSULT (a numeric data item) is 3, because the third argument,
C, has the greatest value.
7.33 ORD-MIN
Description
The ORD-MIN function returns a value that is the ordinal number of the
argument that contains the minimum value.

arg
is an alphabetic, alphanumeric, integer, or numeric argument.
Rules
- The type of this function is integer.
- The arguments must be all alphabetic, all alphanumeric, all
integer, or all numeric, except that integer and numeric arguments can
be mixed and alphabetic and alphanumeric arguments can be mixed.
- The returned value is the ordinal number that corresponds to the
position of the argument having the least value in the argument series.
- The comparisons used to determine the least value are made
according to the rules for simple conditions. (See Chapter 6.)
- If more than one argument has the same least value, the number
returned corresponds to the position of the leftmost argument having
that value.
- If there is only one argument, the value returned is 1.
Example
COMPUTE RSULT = FUNCTION ORD-MIN (A, B, C).
|
A, B, and C are alphanumeric data items one character in length. If the
value "A" is in A, "B" is in B, and "C" is in C, the value returned and
stored in RSULT (a numeric data item) is 1, because the first argument,
A, has the least value.
7.34 PRESENT-VALUE
Description
The PRESENT-VALUE function returns a value that approximates the
present value of a series of future period-end amounts at a discount
rate. The discount rate is specified by the first argument, and the
future period-end amount(s) by one or more subsequent arguments.

rate
is a numeric argument greater than -1 representing the discount rate.
amt
is a numeric argument representing a future period-end amount.
Rules
- The type of this function is numeric.
- The period-end amounts specified must be for periods of equal
duration, and the discount rate must be the rate per period (for
example, if each period is a year, then use the annual discount rate).
- The returned value is an approximation of the summation of a series
of calculations with each term in the following form:
There is one term for each occurrence of amt. The exponent, n, is
incremented from 1 by 1 for each term in the series. If there are four
arguments (rate, amt-1, amt-2, amt-3), the calculation is as follows:
present-value = amt-1 / (1 + rate) ** 1 +
amt-2 / (1 + rate) ** 2 + amt-3 / (1 +
rate) ** 3
|
Example
COMPUTE RSULT = FUNCTION PRESENT-VALUE (DISCOUNT-RATE, 2000).
|
DISCOUNT-RATE and RSULT are numeric data items. If DISCOUNT-RATE has
the value 0.08, the value returned and stored in RSULT is approximately
1851.85.
7.35 RANDOM
Description
The RANDOM function returns a numeric value that is a pseudo-random
number from a rectangular distribution.
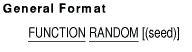
seed
is an optional integer argument with the value of 0 or a positive
integer, used as the seed value to generate a sequence of pseudo-random
numbers. The range of seed values that results in unique sequences of
pseudo-random numbers is 0 through 2147483647.
Rules
- The type of this function is numeric.
- If the optional seed argument is not specified by the first
reference to this function in the run unit, the seed value is 0.
- If any subsequent reference to this function in the run unit does
not specify the seed argument, the value returned is the next number in
the current sequence of pseudo-random numbers.
- If a subsequent reference to this function in the run unit does
specify the seed argument, a new sequence of pseudo-random numbers is
started.
- The returned value is greater than or equal to 0 and less than 1.
- For a given seed value, the sequence of pseudo-random numbers is
always the same.
Example
COMPUTE RSULT-1 = FUNCTION RANDOM (12345).
.
.
.
COMPUTE RSULT-2 = FUNCTION RANDOM.
.
.
.
COMPUTE RSULT-3 = FUNCTION RANDOM (12345).
|
RSULT-1, RSULT-2, and RSULT-3 are numeric data items. Assuming the
three sentences in the example are in the same run unit, the values
returned and stored in RSULT-1 and RSULT-3 are the same. RSULT-2 has a
different value consisting of the next number in the sequence that was
started by the first reference to the function.
7.36 RANGE
Description
The RANGE function returns a value that is equal to the value of the
maximum argument minus the value of the minimum argument.

num
is a numeric or integer argument.
Rules
- The type of this function depends upon the argument types, as
follows:
| Arguments |
Function Type |
|
Integer (all arguments)
|
Integer
|
|
Numeric (some arguments might be integer)
|
Numeric
|
- The returned value is equal to the greatest value in the series of
arguments minus the least value in the series.
- The comparisons used to determine the greatest and least values are
made according to the rules for simple conditions. (See Chapter 6.)
- If only one argument is specified, the value returned is 0.
Example
COMPUTE RSULT = FUNCTION RANGE (4, 8, 10).
|
The value returned and stored in RSULT (a numeric integer data item) is
6.
7.37 REM
Description
The REM function returns a numeric value that is the remainder of the
first argument divided by the second argument.
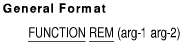
arg-1
is a numeric or integer argument.
arg-2
is a numeric or integer argument whose value cannot be 0.
Rules
- The type of this function is numeric.
- The returned value is the remainder of the first argument divided
by the second argument, and is defined as the following expression:
arg-1 -- (arg-2 * FUNCTION INTEGER-PART (arg-1 /
arg-2))
|
(The INTEGER-PART function returns an integer that is the integer
portion of its argument. See Section 7.18. )
Examples
-
COMPUTE RSULT = FUNCTION REM (3, 2).
|
The value returned and stored in RSULT (a numeric data item) is 1.
-
COMPUTE RSULT = FUNCTION REM (4, 2).
|
The value returned and stored in RSULT is 0.
7.38 REVERSE
Description
The REVERSE function returns a character string of exactly the same
length as the argument and whose characters are exactly the same as
those of the argument, except that they are in reverse order.

arg
is an alphabetic or alphanumeric argument at least one character in
length.
Rules
- The type of this function is alphanumeric.
- If the argument is a character string of length n, the returned
value is a character string of length n.
- When 1 is less than or equal to j and j is less than or equal to n,
the character in position j of the returned value is the character from
position (n--j)+1 of the argument.
Example
MOVE FUNCTION REVERSE (STR) TO RSULT.
|
STR and RSULT are alphanumeric data items four characters in length. If
STR contains the value "ABCD" then "DCBA" is the value returned and
stored in RSULT.
If the value "AB" is moved to the four-character data item STR, then
STR will actually contain "AB " with two trailing spaces. Then the
REVERSE function returns the value " BA" with two leading spaces.
7.39 SIN
Description
The SIN function returns a numeric value that approximates the sine of
an angle or arc, expressed in radians, that is specified by the
argument.

angle
is a numeric argument having the value of the measurement in radians of
an angle or arc.
Rules
- The type of this function is numeric.
- The returned value is the approximation of the sine of angle, and
is greater than or equal to -1 and less than or equal to +1.
Example
COMPUTE SIN-RSLT = FUNCTION SIN (X).
|
If the value of X is 3, the approximate sine of an angle of 3 radians
is moved to SIN-RSLT (a numeric data item).
7.40 SQRT
Description
The SQRT function returns a numeric value that approximates the square
root of the argument.

num
is a numeric or integer argument whose value must be 0 or positive.
Rules
- The type of this function is numeric.
- The returned value is the absolute value of the approximation of
the square root of the argument.
Example
COMPUTE RSULT = FUNCTION SQRT (NUM).
|
NUM and RSULT are numeric data items. If NUM has the value 4, the value
returned and stored in RSULT is 2.
7.41 STANDARD-DEVIATION
Description
The STANDARD-DEVIATION function returns a numeric value that
approximates the standard deviation of its arguments.

arg
is a numeric or integer argument.
Rules
- The type of this function is numeric.
- The returned value is the approximation of the standard deviation
of the argument series.
- The returned value is calculated as follows:
- The difference between each argument's value and the arithmetic
mean (average) of the argument series is calculated and squared.
- The values obtained are then added together. This sum is divided by
the number of values in the argument series.
- The square root of the quotient obtained is then calculated. The
returned value is the absolute value of this square root.
- If the argument series consists of only one value, the returned
value is 0.
Example
COMPUTE RSULT = FUNCTION STANDARD-DEVIATION (A, B, C).
|
A, B, C, and RSULT are numeric data items. If A has the value 1, B has
2, and C has 12, the standard deviation of these values (approximately
4.96655) is returned and stored in RSULT.
7.42 SUM
Description
The SUM function returns a value that is the sum of the arguments.

arg
is an integer or numeric argument.
Rules
- The type of this function depends on the argument types, as follows:
| Arguments |
Function Type |
|
Integer (all arguments)
|
Integer
|
|
Numeric (some arguments might be integer)
|
Numeric
|
- The returned value is the sum of the arguments.
Examples
-
COMPUTE RSULT = FUNCTION SUM (A, B, C).
|
A, B, C, and RSULT are numeric or numeric integer data items. If A has
the value +4, B -2, and C +1, the sum of +3 is the value returned and
stored in RSULT.
-
COMPUTE TOTAL-OUT =
FUNCTION SUM(FUNCTION SQRT(X),
FUNCTION MOD(Y, Z),
A * B,
FUNCTION ACOS(1)).
|
This example shows functions used as arguments to another function. The
data items are all numeric or numeric integer. The value returned and
stored in TOTAL-OUT is the approximate value of the result of adding
the values returned by the functions SQRT, MOD, and ACOS to another
arithmetic expression, A * B.
- The following example shows two arguments that are tables, with
generic (ALL) subscripting, and a third argument that is a literal:
FUNCTION SUM(A(ALL), B(ALL, 2), 4)
|
The number of subscripts shows that A is a one-dimensional table
and B is a two-dimensional table. If A has three occurrences, then
A(ALL) is a set consisting of the elements A(1), A(2), and A(3). If B
has two occurrences in its outer dimension, then B(ALL, 2) is a set
consisting of the elements in B(1, 2) and B(2, 2).
If A has three
elements altogether with the values 2 in A(1), 3 in A(2), and 3 in
A(3), and if B has the values 9 in B(1, 2) and 3 in B(2, 2),
then the value returned is 24---the sum of 2, 3, 3 (from table A), 9, 3
(from table B), and 4 (the third argument).
7.43 TAN
Description
The TAN function returns a numeric value that approximates the tangent
of an angle or arc, expressed in radians, that is specified by the
argument.

arg
is a numeric or integer argument.
Rules
- The type of this function is numeric.
- The returned value is the approximate tangent of the angle
specified.
Example
COMPUTE TAN-RSLT = FUNCTION TAN (X).
|
X and TAN-RSULT are numeric data items. If the value of X is 3, the
approximate tangent of an angle of 3 radians is moved to TAN-RSLT.
7.44 TEST-DATE-YYYYMMDD
Description
The TEST-DATE-YYYYMMDD function tests whether a standard date in the
form YYYYMMDD is a valid date in the Gregorian calendar.
General Format
FUNCTION TEST-DATE-YYYYMMDD ( arg )
|
arg
is an integer.
Rules
- The type of this function is integer.
- If the year is not within the range 1601 through 9999, the
function returns a 1.
Otherwise, if the month is not within the
range 1 through 12, the function returns a 2.
Otherwise, if the
number of days is invalid for the given month, the function returns a
3.
Otherwise, the function returns a 0 to indicate the date is a
valid date in the form YYYYMMDD.
Example
IF FUNCTION TEST-DATE-YYYYMMDD (123456789) = 1
DISPLAY "correct - invalid year (12345)".
IF FUNCTION TEST-DATE-YYYYMMDD (19952020) = 2
DISPLAY "correct - invalid mm (20)".
IF FUNCTION TEST-DATE-YYYYMMDD (19950229) = 3
DISPLAY "correct - invalid dd (29)".
IF FUNCTION TEST-DATE-YYYYMMDD (20040229) = 0
DISPLAY "correct - valid YYYYMMDD".
|
7.45 TEST-DAY-YYYYDDD
Description
The TEST-DAY-YYYYDDD function tests whether a Julian date in the form
YYYYDDD is a valid date in the Gregorian calendar.
General Format
FUNCTION TEST-DAY-YYYYDDD ( arg )
|
arg
is an integer.
Rules
- The type of this function is integer.
- If the year is not within the range 1601 through 9999, the
function returns a 1.
Otherwise, if the number of days is invalid
for the given year, the function returns a 2.
Otherwise, the
function returns a 0 to indicate the date is a valid date in the form
YYYYDDD.
Example
IF FUNCTION TEST-DAY-YYYYDDD (12345678) = 1
DISPLAY "correct - invalid year (12345)".
IF FUNCTION TEST-DAY-YYYYDDD (1995366) = 2
DISPLAY "correct - invalid ddd (366)".
IF FUNCTION TEST-DAY-YYYYDDD (2004366) = 0
DISPLAY "correct - valid YYYYDDD".
|