HP OpenVMS Systems Documentation

OpenVMS VAX RTL Mathematics (MTH$) Manual

Part 2
Scalar MTH$ Reference Section

The Scalar MTH$ Reference Section provides detailed descriptions of the scalar routines provided by the OpenVMS RTL Mathematics (MTH$) facility.

MTH$xACOS

Given the cosine of an angle, the Arc Cosine of Angle Expressed in Radians routine returns that angle (in radians).

Format

MTH$ACOS cosine
MTH$DACOS cosine
MTH$GACOS cosine
Each of the above formats accepts one of the floating-point types as input.
Corresponding JSB Entry Points
MTH$ACOS_R4
MTH$DACOS_R7
MTH$GACOS_R7
Each of the above JSB entry points accepts one of the floating-point types as input.

RETURNS

OpenVMS usage: floating_point

type: F_floating, D_floating, G_floating

access: write only

mechanism: by value

Angle in radians. The angle returned will have a value in the range:
0 <= angle <= Pi sign

MTH$ACOS returns an F-floating number. MTH$DACOS returns a D-floating number. MTH$GACOS returns a G-floating number.

Argument

cosine

OpenVMS usage: floating_point

type: F_floating, D_floating, G_floating

access: read only

mechanism: by reference

The cosine of the angle whose value (in radians) is to be returned. The cosine argument is the address of a floating-point number that is this cosine. The absolute value of cosine must be less than or equal to 1. For MTH$ACOS, cosine specifies an F-floating number. For MTH$DACOS, cosine specifies a D-floating number. For MTH$GACOS, cosine specifies a G-floating number.

Description

The angle in radians whose cosine is X is computed as:

Value of Cosine Value Returned

0 Pi sign/2

1 0

-1 Pi sign

0 < X < 1 zATAN(zSQRT(1-X ²)/X) , where zATAN and zSQRT are the Math Library arc tangent and square root routines, respectively, of the appropriate data type

-1 < X < 0 zATAN(zSQRT(1-X ²)/X) + Pi sign

1 < |X| The error MTH$_INVARGMAT is signaled

See MTH$HACOS for the description of the H-floating point version of this routine.

Condition Values Signaled

SS$_ROPRAND Reserved operand. The MTH$xACOS routine encountered a floating-point reserved operand due to incorrect user input. A floating-point reserved operand is a floating-point datum with a sign bit of 1 and a biased exponent of 0. Floating-point reserved operands are reserved for future use by Compaq.

MTH$_INVARGMAT Invalid argument. The absolute value of cosine is greater than 1. LIB$SIGNAL copies the floating-point reserved operand to the mechanism argument vector CHF$L_MCH_SAVR0/R1. The result is the floating-point reserved operand unless you have written a condition handler to change CHF$L_MCH_SAVR0/R1.

Examples

100 !+ ! This BASIC program demonstrates the use of ! MTH$ACOS. !- EXTERNAL REAL FUNCTION MTH$ACOS DECLARE REAL COS_VALUE, ANGLE 300 INPUT "Cosine value between -1 and +1 "; COS_VALUE 400 IF (COS_VALUE < -1) OR (COS_VALUE > 1) THEN PRINT "Invalid cosine value" GOTO 300 500 ANGLE = MTH$ACOS( COS_VALUE ) PRINT "The angle with that cosine is "; ANGLE; "radians" 32767 END

This BASIC program prompts for a cosine value and determines the angle that has that cosine. The output generated by this program is as follows:
$ RUN ACOS Cosine value between -1 and +1 ? .5 The angle with that cosine is 1.0472 radians

PROGRAM GETANGLE(INPUT,OUTPUT);

{+}
{ This Pascal program uses MTH$ACOS to determine
{ the angle which has the cosine given as input.
{-}

VAR
        COS : REAL;

FUNCTION MTH$ACOS(COS : REAL) : REAL;
        EXTERN;

BEGIN
        WRITE('Cosine value between -1 and +1:  ');
        READ (COS);
        WRITELN('The angle with that cosine is ', MTH$ACOS(COS),
        ' radians');
END.

This Pascal program prompts for a cosine value and determines the angle that has that cosine. The output generated by this program is as follows:
$ RUN ACOS Cosine value between -1 and +1: .5 The angle with that cosine is 1.04720E+00 radians

MTH$xACOSD

Given the cosine of an angle, the Arc Cosine of Angle Expressed in Degrees routine returns that angle (in degrees).

Format

MTH$ACOSD cosine
MTH$DACOSD cosine
MTH$GACOSD cosine
Each of the above formats accepts one of the floating-point types as input.
Corresponding JSB Entry Points
MTH$ACOSD_R4
MTH$DACOSD_R7
MTH$GACOSD_R7
Each of the above JSB entry points accepts one of the floating-point types as input.

RETURNS

OpenVMS usage: floating_point

type: F_floating, D_floating, G_floating

access: write only

mechanism: by value

Angle in degrees. The angle returned will have a value in the range:
0 <= angle <= 180
MTH$ACOSD returns an F-floating number. MTH$DACOSD returns a D-floating number. MTH$GACOSD returns a G-floating number.

Argument

cosine

OpenVMS usage: floating_point

type: F_floating, G_floating, D_floating

access: read only

mechanism: by reference

Cosine of the angle whose value (in degrees) is to be returned. The cosine argument is the address of a floating-point number that is this cosine. The absolute value of cosine must be less than or equal to 1. For MTH$ACOSD, cosine specifies an F-floating number. For MTH$DACOSD, cosine specifies a D-floating number. For MTH$GACOSD, cosine specifies a G-floating number.

Description

The angle in degrees whose cosine is X is computed as:

Value of Cosine Angle Returned

0 90

1 0

-1 180

0 < X < 1 zATAND(zSQRT(1-X ²)/X) , where zATAND and zSQRT are the Math Library arc tangent and square root routines, respectively, of the appropriate data type

-1 < X < 0 zATAND(zSQRT(1-X ²)/X) + 180

1 < |X| The error MTH$_INVARGMAT is signaled

See MTH$HACOSD for the description of the H-floating point version of this routine.

Condition Values Signaled

SS$_ROPRAND Reserved operand. The MTH$xACOSD routine encountered a floating-point reserved operand due to incorrect user input. A floating-point reserved operand is a floating-point datum with a sign bit of 1 and a biased exponent of 0. Floating-point reserved operands are reserved for future use by Compaq.

MTH$_INVARGMAT Invalid argument. The absolute value of cosine is greater than 1. LIB$SIGNAL copies the floating-point reserved operand to the mechanism argument vector CHF$L_MCH_SAVR0/R1. The result is the floating-point reserved operand unless you have written a condition handler to change CHF$L_MCH_SAVR0/R1.

Example

PROGRAM ACOSD(INPUT,OUTPUT);
{+}
{ This Pascal program demonstrates the use of MTH$ACOSD.
{-}
FUNCTION MTH$ACOSD(COS : REAL): REAL; EXTERN;

VAR
  COSINE : REAL;
  RET_STATUS : REAL;

BEGIN
  COSINE := 0.5;
  RET_STATUS := MTH$ACOSD(COSINE);
  WRITELN('The angle, in degrees, is: ', RET_STATUS);
END.

The output generated by this Pascal example program is as follows:
The angle, expressed in degrees, is: 6.00000E+01

MTH$xASIN

Given the sine of an angle, the Arc Sine in Radians routine returns that angle (in radians).

Format

MTH$ASIN sine
MTH$DASIN sine
MTH$GASIN sine
Each of the above formats accepts one of the floating-point types as input.
Corresponding JSB Entry Points
MTH$ASIN_R4
MTH$DASIN_R7
MTH$GASIN_R7
Each of the above JSB entry points accepts one of the floating-point types as input.

RETURNS

OpenVMS usage: floating_point

type: F_floating, D_floating, G_floating

access: write only

mechanism: by value

Angle in radians. The angle returned will have a value in the range:
-Pi sign/2 <= angle <= Pi sign/2

MTH$ASIN returns an F-floating number. MTH$DASIN returns a D-floating number. MTH$GASIN returns a G-floating number.

Argument

sine

OpenVMS usage: floating_point

type: F_floating, D_floating, G_floating

access: read only

mechanism: by reference

The sine of the angle whose value (in radians) is to be returned. The sine argument is the address of a floating-point number that is this sine. The absolute value of sine must be less than or equal to 1. For MTH$ASIN, sine specifies an F-floating number. For MTH$DASIN, sine specifies a D-floating number. For MTH$GASIN, sine specifies a G-floating number.

Description

The angle in radians whose sine is X is computed as:

Value of Sine Angle Returned

0 0

1 Pi sign/2

-1 -Pi sign/2

0 < |X| < 1 zATAN(X/zSQRT(1-X ²)) , where zATAN and zSQRT are the Math Library arc tangent and square root routines, respectively, of the appropriate data type

1 < |X| The error MTH$_INVARGMAT is signaled

See MTH$HASIN for the description of the H-floating point version of this routine.

Condition Values Signaled

SS$_ROPRAND Reserved operand. The MTH$xASIN routine encountered a floating-point reserved operand due to incorrect user input. A floating-point reserved operand is a floating-point datum with a sign bit of 1 and a biased exponent of 0. Floating-point reserved operands are reserved for future use by Compaq.

MTH$_INVARGMAT Invalid argument. The absolute value of sine is greater than 1. LIB$SIGNAL copies the floating-point reserved operand to the mechanism argument vector CHF$L_MCH_SAVR0/R1. The result is the floating-point reserved operand unless you have written a condition handler to change CHF$L_MCH_SAVR0/R1.

MTH$xASIND

Given the sine of an angle, the Arc Sine in Degrees routine returns that angle (in degrees).

Format

MTH$ASIND sine
MTH$DASIND sine
MTH$GASIND sine
Each of the above formats accepts one of the floating-point types as input.
Corresponding JSB Entry Points
MTH$ASIND_R4
MTH$DASIND_R7
MTH$GASIND_R7
Each of the above JSB entry points accepts one of the floating-point types as input.

RETURNS

OpenVMS usage: floating_point

type: F_floating, D_floating, G_floating

access: write only

mechanism: by value

Angle in degrees. The angle returned will have a value in the range:
-90 <= angle <= 90

MTH$ASIND returns an F-floating number. MTH$DASIND returns a D-floating number. MTH$GASIND returns a G-floating number.

Argument

sine

OpenVMS usage: floating_point

type: F_floating, D_floating, G_floating

access: read only

mechanism: by reference

Sine of the angle whose value (in degrees) is to be returned. The sine argument is the address of a floating-point number that is this sine. The absolute value of sine must be less than or equal to 1. For MTH$ASIND, sine specifies an F-floating number. For MTH$DASIND, sine specifies a D-floating number. For MTH$GASIND, sine specifies a G-floating number.

Description

The angle in degrees whose sine is X is computed as:

Value of Sine Value Returned

0 0

1 90

-1 -90

0 < |X| < 1 zATAND(X/zSQRT(1-X ²)) , where zATAND and zSQRT are the Math Library arc tangent and square root routines, respectively, of the appropriate data type

1 < |X| The error MTH$_INVARGMAT is signaled

See MTH$HASIND for the description of the H-floating version of this routine.

Condition Values Signaled

SS$_ROPRAND Reserved operand. The MTH$xASIND routine encountered a floating-point reserved operand due to incorrect user input. A floating-point reserved operand is a floating-point datum with a sign bit of 1 and a biased exponent of 0. Floating-point reserved operands are reserved for future use by Compaq.

MTH$_INVARGMAT Invalid argument. The absolute value of sine is greater than 1. LIB$SIGNAL copies the floating-point reserved operand to the mechanism argument vector CHF$L_MCH_SAVR0/R1. The result is the floating-point reserved operand unless you have written a condition handler to change CHF$L_MCH_SAVR0/R1.

MTH$xATAN

Given the tangent of an angle, the Arc Tangent in Radians routine returns that angle (in radians).

Format

MTH$ATAN tangent
MTH$DATAN tangent
MTH$GATAN tangent
Each of the above formats accepts one of the floating-point types as input.
Corresponding JSB Entry Points
MTH$ATAN_R4
MTH$DATAN_R7
MTH$GATAN_R7
Each of the above JSB entry points accepts one of the floating-point types as input.

RETURNS

OpenVMS usage: floating_point

type: F_floating, D_floating, G_floating

access: write only

mechanism: by value

Angle in radians. The angle returned will have a value in the range:

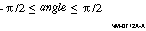
MTH$ATAN returns an F-floating number. MTH$DATAN returns a D-floating number. MTH$GATAN returns a G-floating number.

Argument

tangent

OpenVMS usage: floating_point

type: F_floating, D_floating, G_floating

access: read only

mechanism: by reference

The tangent of the angle whose value (in radians) is to be returned. The tangent argument is the address of a floating-point number that is this tangent. For MTH$ATAN, tangent specifies an F-floating number. For MTH$DATAN, tangent specifies a D-floating number. For MTH$GATAN, tangent specifies a G-floating number.

Description

In radians, the computation of the arc tangent function is based on the following identities:

arctan(X) = X - X ³/3 + X ⁵/5 - X ⁷/7 + ...

arctan(X) = X + X*Q(X ²),
where Q(Y) = - Y/3 + Y ²/5 - Y ³/7 + ...

arctan(X) = X*P(X ²),
where P(Y) = 1 - Y/3 + Y ²/5 - Y ³/7 + ...

arctan(X) = Pi sign/2 - arctan(1/X)

arctan(X) = arctan(A) + arctan((X-A)/(1+A*X))
for any real A

The angle in radians whose tangent is X is computed as:

Value of X Angle Returned

0 <= X <= 3/32 X + X * Q(X ²)

3/32 < X <= 11 ATAN(A) + V* (P(V ²)), where A and ATAN(A) are chosen by table lookup and V = (X - A)/(1 + A*X)

11 < X Pi sign/2 - W* (P(W ²)) where W = 1/X

X < 0 -zATAN(|X|)

See MTH$HATAN for the description of the H-floating point version of this routine.

Condition Value Signaled

SS$_ROPRAND Reserved operand. The MTH$xATAN routine encountered a floating-point reserved operand due to incorrect user input. A floating-point reserved operand is a floating-point datum with a sign bit of 1 and a biased exponent of 0. Floating-point reserved operands are reserved for future use by Compaq.

Contents

Index

HP OpenVMS Systems Documentation

OpenVMS VAX RTL Mathematics (MTH$) Manual

Part 2Scalar MTH$ Reference Section

MTH$xACOS

Format

Corresponding JSB Entry Points

RETURNS

Argument

cosine

Description

Condition Values Signaled

Examples

MTH$xACOSD

Format

Corresponding JSB Entry Points

RETURNS

Argument

cosine

Description

Condition Values Signaled

Example

MTH$xASIN

Format

Corresponding JSB Entry Points

RETURNS

Argument

sine

Description

Condition Values Signaled

MTH$xASIND

Format

Corresponding JSB Entry Points

RETURNS

Argument

sine

Description

Condition Values Signaled

MTH$xATAN

Format

Corresponding JSB Entry Points

RETURNS

Argument

tangent

Description

Condition Value Signaled

Part 2
Scalar MTH$ Reference Section