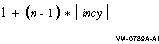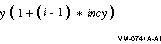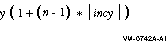|
OpenVMS VAX RTL Mathematics (MTH$) Manual
If n is less than or equal to 0, then
x and y are unchanged. If any element
of x shares a memory location with an element of y , the results are
unpredictable.
On exit, y is an array of length at least:
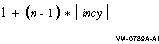
where:
|
n
|
=
|
number of vector elements specified in
n
|
|
incy
|
=
|
increment argument for the array
y specified in
incy
|
After the call to BLAS1$VxSWAP, n elements of the
array specified by x are interchanged with
n elements of the array specified by
y.
incy
| OpenVMS usage: |
longword_signed |
| type: |
longword integer (signed) |
| access: |
read only |
| mechanism: |
by reference |
Increment argument for the array y. The
incy argument is the address of a signed longword
integer containing the increment argument. If incy is
greater than or equal to 0, then y is referenced forward in array
y; that is, y[i] is referenced in:
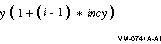
where:
|
y
|
=
|
array specified in
y
|
|
i
|
=
|
element of the vector y
|
|
incy
|
=
|
increment argument for the array
y specified in
incy
|
If incy is less than 0, then y is referenced backward
in array y; that is, y[i] is referenced in:
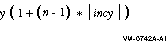
where:
|
y
|
=
|
array specified in
y
|
|
n
|
=
|
number of vector elements specified in
n
|
|
i
|
=
|
element of the vector y
|
|
incy
|
=
|
increment argument for the array
y specified in
incy
|
Description
BLAS1$VSSWAP, BLAS1$VDSWAP, BLAS1$VCSWAP, and BLAS1$VZSWAP swap
n elements of the vector x with the vector y . Vectors x and y
contain n elements that are accessed from arrays
x and y by stepping
incx and incy elements at a time.
Both x and y are real or complex single-precision or double-precision
(D and G) n-element vectors. The vectors can be rows or
columns of a matrix. Both forward and backward indexing are permitted.
You can use the routine BLAS1$VxSWAP to invert the storage of elements
of a vector within itself. If incx is greater than 0,
then x[i] can be moved from location
x(1+(i-1)*incx) to x(1+(n-i)*incx)
The following code fragment inverts the storage of elements of a vector
within itself:
NN = N/2
LHALF = 1+(N-NN)*INCX
CALL BLAS1$VxSWAP(NN,X,INCX,X(LHALF),-INCX)
|
BLAS1$VxSWAP does not check for a reserved operand.
Example
|
C
C To swap the contents of vectors x and y:
C
INTEGER INCX,INCY,N
REAL X(20),Y(20)
INCX = 1
INCY = 1
N = 20
CALL BLAS1$VSSWAP(N,X,INCX,Y,INCY)
C
C To invert the order of storage of the elements of x within
C itself; that is, to move x(1),...,x(100) to x(100),...,x(1):
C
INCX = 1
INCY = -1
N = 50
CALL BLAS1$VSSWAP(N,X,INCX,X(51),INCY)
|
MTH$VxFOLRy_MA_V15
The First Order Linear Recurrence --- Multiplication and Addition
routine provides a vectorized algorithm for the linear recurrence
relation that includes both multiplication and addition operations.
Format
MTH$VJFOLRP_MA_V15 n,a,inca,b,incb,c,incc
MTH$VFFOLRP_MA_V15 n,a,inca,b,incb,c,incc
MTH$VDFOLRP_MA_V15 n,a,inca,b,incb,c,incc
MTH$VGFOLRP_MA_V15 n,a,inca,b,incb,c,incc
MTH$VJFOLRN_MA_V15 n,a,inca,b,incb,c,incc
MTH$VFFOLRN_MA_V15 n,a,inca,b,incb,c,incc
MTH$VDFOLRN_MA_V15 n,a,inca,b,incb,c,incc
MTH$VGFOLRN_MA_V15 n,a,inca,b,incb,c,incc
To obtain one of the preceding formats, substitute the following for
x and y in MTH$VxFOLRy_MA_V15:
|
x
|
=
|
J for longword integer, F for F-floating, D for D-floating, G for
G-floating
|
|
y
|
=
|
P for a positive recursion element, N for a negative recursion element
|
RETURNS
None.
Arguments
n
| OpenVMS usage: |
longword_signed |
| type: |
longword integer (signed) |
| access: |
read only |
| mechanism: |
by reference |
Length of the linear recurrence. The n argument is the
address of a signed longword integer containing the length.
a
| OpenVMS usage: |
longword_signed or floating_point |
| type: |
longword integer (signed), F_floating, D_floating, or
G_floating |
| access: |
read only |
| mechanism: |
by reference, array reference |
Array of length at least:
1+(n-1)*inca
where:
|
n
|
=
|
length of the linear recurrence specified in
n
|
|
inca
|
=
|
increment argument for the array
a specified in
inca
|
The a argument is the address of a longword integer or
floating-point that is this array.
inca
| OpenVMS usage: |
longword_signed |
| type: |
longword integer (signed) |
| access: |
read only |
| mechanism: |
by reference |
Increment argument for the array a. The
inca argument is the address of a signed longword
integer containing the increment argument. For contiguous elements,
specify 1 for inca.
b
| OpenVMS usage: |
longword_signed or floating_point |
| type: |
longword integer (signed), F_floating, D_floating, or
G_floating |
| access: |
read only |
| mechanism: |
by reference, array reference |
Array of length at least:
1+(n-1)*incb
where:
|
n
|
=
|
length of the linear recurrence specified in
n
|
|
incb
|
=
|
increment argument for the array
b specified in
incb
|
The b argument is the address of a longword integer or
floating-point number that is this array.
incb
| OpenVMS usage: |
longword_signed |
| type: |
longword integer (signed) |
| access: |
read only |
| mechanism: |
by reference |
Increment argument for the array b. The
incb argument is the address of a signed longword
integer containing the increment argument. For contiguous elements,
specify 1 for incb.
c
| OpenVMS usage: |
longword_signed or floating_point |
| type: |
longword integer (signed), F_floating, D_floating, or
G_floating |
| access: |
modify |
| mechanism: |
by reference, array reference |
Array of length at least:
1+n*incc
where:
|
n
|
=
|
length of the linear recurrence specified in
n
|
|
incc
|
=
|
increment argument for the array
c specified in
incc
|
The c argument is the address of a longword integer or
floating-point number that is this array.
incc
| OpenVMS usage: |
longword_signed |
| type: |
longword integer (signed) |
| access: |
read only |
| mechanism: |
by reference |
Increment argument for the array c. The
incc argument is the address of a signed longword
integer containing the increment argument. For contiguous elements,
specify 1 for incc. Do not specify 0 for
incc.
Description
MTH$VxFOLRy_MA_V15 is a group of routines that provides a vectorized
algorithm for computing the following linear recurrence relation:
C(I+1) = +/-C(I) * A(I) + B(I)
Note
Save the contents of vector registers V0 through V15 before you call
this routine.
|
Call this routine to utilize vector hardware when computing the
recurrence. As an example, the call from Compaq Fortran is as follows:
K1 = ....
K2 = ....
K3 = ....
CALL MTH$VxFOLRy_MA_V15(N,A(K1),INCA,B(K2),INCB,C(K3),INCC)
|
The preceding Fortran call replaces the following loop:
K1 = ....
K2 = ....
K3 = ....
DO I = 1, N
C(K3+I*INCC) = {+/-}C(K3+(I-1)*INCC) * A(K1+(I-1)*INCA)
+ B(K2+(I-1)*INCB)
ENDDO
|
The arrays used in a FOLR expression must be of the same data type in
order to be vectorized and user callable. The MTH$ FOLR routines assume
that all of the arrays are of the same data type.
This group of routines, MTH$VxFOLRy_MA_V15 (and also MTH$VxFOLRy_z_V8)
save the result of each iteration of the linear recurrence relation in
an array. This is different from the behavior of MTH$VxFOLRLy_MA_V5 and
MTH$VxFOLRLy_z_V2, which return only the result of the last iteration
of the linear recurrence relation.
For the output array (c), the increment argument
(incc) cannot be 0. However, you can specify 0 for the
input increment arguments (inca and
incb). In that case, the input will be treated as a
scalar value and broadcast to a vector input with all vector elements
equal to the scalar value.
In MTH$VxFOLRy_MA_V15, array c can overlap array
a and array b, or both, as long as
the address of array element c[x] is not also the address of an element
of a or b that will be referenced at
a future time in the recurrence relation. For example, in the following
code fragment you must ensure that the address of c(1+i*incc) does not
equal the address of either a(j*inca) or b(k*incb) for:
1<=i<= n and j=>i+1 .
DO I = 1,N
C(1+I*INCC) = C(1+(I-1)*INCC) * A(1+(I-1)*INCA) + B(1+(I-1)*INCB)
ENDDO
|
Examples
| #1 |
C
C The following Fortran loop computes a linear recurrence.
C
INTEGER I
DIMENSION A(200), B(50), C(50)
EQUIVALENCE (B,C)
:
C(4) = ....
DO I = 5, 50
C(I) = C((I-1)) * A(I*3) + B(I)
ENDDO
C
C This call from Fortran to a FOLR routine replaces the preceding loop.
C
DIMENSION A(200), B(50), C(50)
EQUIVALENCE (B,C)
:
C(4) = ....
CALL MTH$VFFOLRP_MA_V15(46, A(15), 3, B(5), 1, C(4), 1)
|
| #2 |
C
C The following Fortran loop computes a linear recurrence.
C
INTEGER K,N,INCA,INCB,INCC,I
DIMENSION A(30), B(6), C(50)
K = 44
N = 6
INCA = 5
INCB = 1
INCC = 1
DO I = 1, N
C(K+I*INCC) = -C(K+(I-1)*INCC) * A(I*INCA) + B(I*INCB)
ENDDO
C
C This call from Fortran to a FOLR routine replaces the preceding loop.
C
INTEGER K,N,INCA,INCB,INCC
DIMENSION A(30), B(6), C(50)
K = 44
N = 6
INCA = 5
INCB = 1
INCC = 1
CALL MTH$VFFOLRN_MA_V15(N, A(INCA), INCA, B(INCB), INCB, C(K), INCC)
|
MTH$VxFOLRy_z_V8
The First Order Linear Recurrence --- Multiplication or Addition
routine provides a vectorized algorithm for the linear recurrence
relation that includes either a multiplication or an addition
operation, but not both.
Format
MTH$VJFOLRP_M_V8 n,a,inca,b,incb
MTH$VFFOLRP_M_V8 n,a,inca,b,incb
MTH$VDFOLRP_M_V8 n,a,inca,b,incb
MTH$VGFOLRP_M_V8 n,a,inca,b,incb
MTH$VJFOLRN_M_V8 n,a,inca,b,incb
MTH$VFFOLRN_M_V8 n,a,inca,b,incb
MTH$VDFOLRN_M_V8 n,a,inca,b,incb
MTH$VGFOLRN_M_V8 n,a,inca,b,incb
MTH$VJFOLRP_A_V8 n,a,inca,b,incb
MTH$VFFOLRP_A_V8 n,a,inca,b,incb
MTH$VDFOLRP_A_V8 n,a,inca,b,incb
MTH$VGFOLRP_A_V8 n,a,inca,b,incb
MTH$VJFOLRN_A_V8 n,a,inca,b,incb
MTH$VFFOLRN_A_V8 n,a,inca,b,incb
MTH$VDFOLRN_A_V8 n,a,inca,b,incb
MTH$VGFOLRN_A_V8 n,a,inca,b,incb
To obtain one of the preceding formats, substitute the following for
x, y, and z in MTH$VxFOLRy_z_V8:
|
x
|
=
|
J for longword integer, F for F-floating, D for D-floating, G for
G-floating
|
|
y
|
=
|
P for a positive recursion element, N for a negative recursion element
|
|
z
|
=
|
M for multiplication, A for addition
|
RETURNS
None.
Arguments
n
| OpenVMS usage: |
longword_signed |
| type: |
longword integer (signed) |
| access: |
read only |
| mechanism: |
by reference |
Length of the linear recurrence. The n argument is the
address of a signed longword integer containing the length.
a
| OpenVMS usage: |
longword_signed or floating_point |
| type: |
longword integer (signed), F_floating, D_floating, or
G_floating |
| access: |
read only |
| mechanism: |
by reference, array reference |
Array of length at least:
1+(n-1)*inca
where:
|
n
|
=
|
length of the linear recurrence specified in
n
|
|
inca
|
=
|
increment argument for the array
a specified in
inca
|
The a argument is the address of a longword integer or
floating-point that is this array.
inca
| OpenVMS usage: |
longword_signed |
| type: |
longword integer (signed) |
| access: |
read only |
| mechanism: |
by reference |
Increment argument for the array a. The
inca argument is the address of a signed longword
integer containing the increment argument. For contiguous elements,
specify 1 for inca.
b
| OpenVMS usage: |
longword_signed or floating_point |
| type: |
longword integer (signed), F_floating, D_floating, or
G_floating |
| access: |
modify |
| mechanism: |
by reference, array reference |
Array of length at least:
1+(n-1)*incb
where:
|
n
|
=
|
length of the linear recurrence specified in
n
|
|
incb
|
=
|
increment argument for the array
b specified in
incb
|
The b argument is the address of a longword integer or
floating-point number that is this array.
incb
| OpenVMS usage: |
longword_signed |
| type: |
longword integer (signed) |
| access: |
read only |
| mechanism: |
by reference |
Increment argument for the array b. The
incb argument is the address of a signed longword
integer containing the increment argument. For contiguous elements,
specify 1 for incb.
Description
MTH$VxFOLRy_z_V8 is a group of routines that provide a vectorized
algorithm for computing one of the following linear recurrence
relations:
B(I) = +/-B(I-1) * A(I)
or
B(I) = +/-B(I-1) + A(I)
For the first relation, specify M for z in the routine name to
denote multiplication; for the second relation, specify A for
z in the routine name to denote addition.
Note
Save the contents of vector registers V0 through V8 before you call
this routine.
|
Call this routine to utilize vector hardware when computing the
recurrence. As an example, the call from Compaq Fortran is as follows:
CALL MTH$VxFOLRy_z_V8(N,A(K1),INCA,B(K2),INCB)
|
The preceding Fortran call replaces the following loop:
K1 = ....
K2 = ....
DO I = 1, N
B(K2+I*INCB) = {+/-}B(K2+(I-1)*INCB) {+/*} A(K1+(I-1)*INCA)
ENDDO
|
The arrays used in a FOLR expression must be of the same data type in
order to be vectorized and user callable. The MTH$ FOLR routines assume
that all of the arrays are of the same data type.
This group of routines, MTH$VxFOLRy_z_V8 (and also MTH$VxFOLRy_MA_V15)
save the result of each iteration of the linear recurrence relation in
an array. This is different from the behavior of MTH$VxFOLRLy_MA_V5 and
MTH$VxFOLRLy_z_V2, which return only the result of the last iteration
of the linear recurrence relation.
For the output array (b), the increment argument
(incb) cannot be 0. However, you can specify 0 for the
input increment argument (inca). In that case, the
input will be treated as a scalar and broadcast to a vector input with
all vector elements equal to the scalar value.
Examples
| #1 |
C
C The following Fortran loop computes
C a linear recurrence.
C
C D_FLOAT
INTEGER N,INCA,INCB,I
DIMENSION A(30), B(13)
N = 6
INCA = 5
INCB = 2
DO I = 1, N
B(1+I*INCB) = -B(1+(I-1)*INCB) * A(I*INCA)
ENDDO
C
C The following call from Fortran to a FOLR
C routine replaces the preceding loop.
C
C D_FLOAT
INTEGER N,INCA,INCB
REAL*8 A(30), B(13)
N = 6
INCA = 5
INCB = 2
CALL MTH$VDFOLRN_M_V8(N, A(INCA), INCA, B(1), INCB)
|
| #2 |
C
C The following Fortran loop computes
C a linear recurrence.
C
C G_FLOAT
INTEGER N,INCA,INCB
DIMENSION A(30), B(13)
N = 5
INCA = 5
INCB = 2
DO I = 2, N
B(1+I*INCB) = B((I-1)*INCB) + A(I*INCA)
ENDDO
C
C The following call from Fortran to a FOLR
C routine replaces the preceding loop.
C
C G_FLOAT
INTEGER N,INCA,INCB
REAL*8 A(30), B(13)
N = 5
INCA = 5
INCB = 2
CALL MTH$VGFOLRP_A_V8(N, A(INCA), INCA, B(INCB), INCB)
|
|