| Previous | Contents | Index |
BASIC lets you control the compilation of a program by creating and testing lexical constants. You create and assign values to lexical constants with the %LET directive. These constants are always LONG integers.
You control the compilation by using the %IF-%THEN-%ELSE-%END %IF directive to test these lexical constants. Thus, you can conditionally:
BASIC also supplies the lexical built-in function %VARIANT that can be used to conditionally control compilation.
%IF-%THEN-%ELSE-%END %IF uses lexical expressions to determine whether to execute directives in the %THEN clause or the %ELSE clause. The following sections describe the use of:
The %LET directive creates and assigns values to lexical constants. Lexical constants are always LONG integers. These constants control the execution of the %IF-%THEN-%ELSE-%END %IF directive.
All lexical constants must be created with %LET before they can be used in a %IF-%THEN-%ELSE-%END %IF directive, and each lexical constant must be created with a separate %LET directive. All lexical constant names must also be preceded by a percent sign and cannot end with a dollar sign or percent sign.
A lexical expression can be any of the following:
The %LET directive lets you create constants that control conditional compilation. For example:
%LET %debug_on = 0% |
See Section 17.4.5 for an example of using %LET with %IF-%THEN-%ELSE.
17.4.2 %VARIANT Directive
The %VARIANT directive is a built-in lexical function that returns an integer. The value of this returned integer is determined by:
The %VARIANT function returns the variant value set with either of these methods.
The default value for the %VARIANT function is zero. See Section 17.4.5
for an example of controlling compilation with %VARIANT.
17.4.3 %ABORT Directive
The %ABORT directive terminates the compilation and displays a message you provide.
The text must be a quoted string literal. This information is displayed
to SYS$ERROR and in the compilation listing if one is being created.
BASIC stops the compilation and terminates the listing file as soon as
it encounters a %ABORT directive, and so BASIC does not perform syntax
checking on the remainder of the program. See Section 17.4.5 for an
example of using %ABORT.
17.4.4 %PRINT Directive
The %PRINT directive allows you to insert a message into your source code that the BASIC compiler displays at compile time.
The text must be a quoted string literal. This information is displayed
to SYS$ERROR and in the compilation listing if one is being created.
BASIC prints the message specified as soon as it encounters a %PRINT
directive. See Section 17.4.5 for an example of using %PRINT.
17.4.5 %IF-%THEN-%ELSE-%END %IF Directive
The %IF-%THEN-%ELSE-%END %IF directive lets you do the following things conditionally:
This directive differs from all others in that it can appear anywhere in a program where a space is allowed, except within a quoted string.
You must include %END %IF. Otherwise, the rest of the source program becomes part of the %THEN or %ELSE clause. You must also include a lexical expression and some BASIC source code.
The truth or falsity of the lexical expression determines whether BASIC compiles the source code in the %THEN clause or the %ELSE clause. If the lexical expression is true, BASIC does not compile the source code in the %ELSE clause. If the lexical expression is false, BASIC does not compile the source code in the %THEN clause. However, BASIC does check for lexical errors (such as illegally formed numeric constants) in the uncompiled block of code. If an uncompiled block of code contains a lexical error, BASIC signals an error.
Even though BASIC compiles only one block of code in an %IF-%THEN-%ELSE-%END-%IF directive, you cannot use the same line number in both a %THEN block and an %ELSE block. If you specify the same line number, the first occurrence of the line number is replaced by the second when the program is compiled.
The following example uses the %VARIANT directive, which returns the value set by the SET VARIANT command or /VARIANT qualifier:
%IF (%VARIANT = 2%) %THEN DECLARE LONG int_array(100) %ELSE DECLARE WORD int_array(100) %END %IF |
This directive allows for two possibilities. If you compile this program with a /VARIANT=2 qualifier, then BASIC creates an array of longword integers. If you compile this program with any other variant value, BASIC creates an array of word integers.
Because %IF can appear within a program line, you can express the same directive this way:
DECLARE %IF (%VARIANT=2%) %THEN LONG %ELSE WORD %END %IF int_array(100) |
A %THEN or %ELSE clause can also contain other compiler directives. For example, the following program creates the lexical constant %my_constant and assigns it a value of 8. The %IF directive evaluates the conditional expression ((%my_constant + %VARIANT) >= 10%). If this expression is true, BASIC executes the %THEN clause, aborting the compilation and issuing an error message. If the expression is false, BASIC prints the specified message and continues to compile your program without aborting the compilation.
%LET %my_constant = 8%
%IF ( (%my_constant + %VARIANT) >= 10% )%THEN
%ABORT "Cannot compile with VARIANT >= 2"
%ELSE
%PRINT "Successful Compilation"
%END %IF
|
The compilation listing shows you which clause was actually compiled.
17.4.6 %DEFINE and %UNDEFINE Directives
The %DEFINE directive allows you to assign a value to an identifier. The %UNDEFINE directive will remove the value.
The representation of this value stays in force until a corresponding
%UNDEFINE directive or the end of the source module is encountered.
17.5 Record Dependency Relationships in CDD/Repository
By using the %INCLUDE %FROM %CDD or the %REPORT %DEPENDENCY directives in conjunction with the /DEPENDENCY_DATA qualifier in the BASIC command, you can record dependency relationships in a CDO dictionary between a compiled module entity and included records or other referenced dictionary entities.
See Chapter 22 for more information about record dependency relationships.
This chapter describes how Compaq BASIC represents data stored in memory. Alpha BASIC refers to Compaq BASIC for OpenVMS Alpha, and VAX BASIC refers to Compaq BASIC for OpenVMS VAX.
The following sections discuss four types of data representation:
integer, float, decimal, and string.
18.1 Integer Format
There are four ways in which integer data can be represented, depending
on the size of the data to be stored: byte, word, longword, and
quadword. Negative integer values are stored in two's complement
format. The following sections describe each of these formats.
18.1.1 Byte-Length Integer Format
Byte-length integers are in the range -128 to 127 and are stored as 1 byte (8 bits), starting on an arbitrary byte boundary. Bits are labeled from the right, 0 to 7, as in Figure 18-1.
Figure 18-1 Byte-Length Integer Format

Word-length integers are in the range -32768 to 32767 and are stored as two contiguous bytes, starting on an arbitrary byte boundary. Bits are labeled from the right, 0 to 15, as in Figure 18-2.
Figure 18-2 Word-Length Integer Format
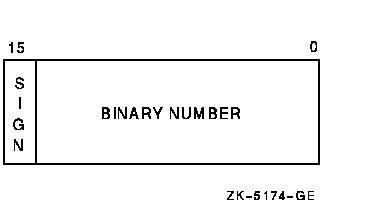
Longword integers are stored as four contiguous bytes, starting on an arbitrary byte boundary. Values are in the range -2147483648 to 2147483647. See Figure 18-3.
Figure 18-3 Longword Integer Format
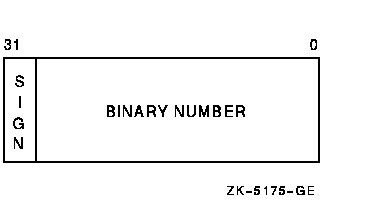
Quadword integers are stored as eight contiguous bytes, starting on an arbitrary byte boundary. Values are in the range -9223372036854775808 to 9223372036854775807. See Figure 18-4.
Figure 18-4 Quadword Integer Format
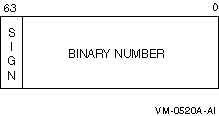
The compiler incorrectly gives an integer overflow message when the most negative integer constants are used, as follows:
BYTE -128% WORD -32768% LONG -2147483648% QUAD -9223372036854775808% |
The workaround is to use the appropriate expression from the following:
BYTE -127% - 1% WORD -32767% - 1% LONG -2147483647% - 1% QUAD -9223372036854775807% - 1% |
Real numbers, like integers, can be represented in varying formats,
depending on the size of the data to be stored. These formats include
SINGLE floating-point, DOUBLE floating-point, GFLOAT floating-point,
HFLOAT floating-point (VAX BASIC only), SFLOAT floating-point
(Alpha BASIC only), TFLOAT floating-point (Alpha BASIC only),
XFLOAT floating-point (Alpha BASIC only), and packed DECIMAL format.
The following sections describe each of these formats.
18.2.1 SINGLE Floating-Point Number Format (F_floating)
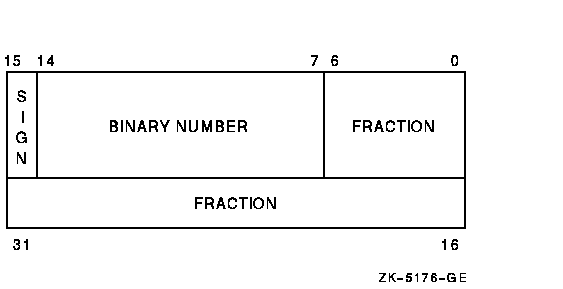
F_floating (single-precision) floating-point numbers are stored as four contiguous bytes, starting on an arbitrary byte boundary. Bits are labeled from the right, 0 to 31.
The format for single-precision is sign magnitude, with bit 15 the sign bit, bits 14 to 7 an excess-128 binary exponent, and bits 6 to 0 and 31 to 16 a normalized 24-bit fraction with the redundant, most significant fraction bit not represented. See Figure 18-5 for the format. The 8-bit exponent field encodes the values from 0 to 255, inclusively.
An exponent value of 0 together with a sign bit of 0 indicates that the F_floating number has a value of 0. Exponent values from 1 to 255 indicate true binary exponents of -127 to 127. An exponent value of 0, together with a sign bit of 1, is taken as reserved. (Floating-point instructions processing a reserved operand take a reserved operand fault.) The magnitude of an F_floating number is in the approximate range .29 * 10-38 to 1.7 * 1038. The precision of an F_floating number is approximately one part in 223 (approximately 7 decimal digits).
Figure 18-5 Single-Precision Real Number Format
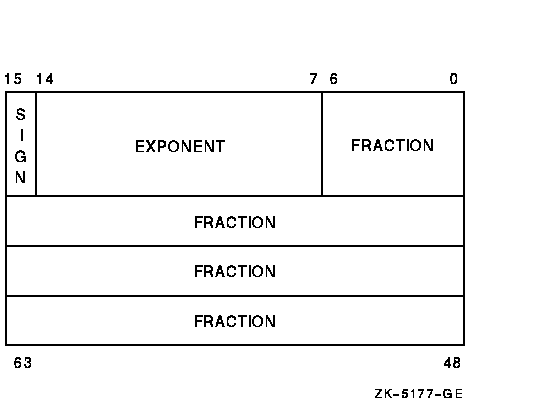
Double-precision real number format consists of eight contiguous bytes, starting on an arbitrary byte boundary. Bits are labeled from the right, 0 to 63, as in Figure 18-6. The form of a D_floating number is identical to the F_floating form, except for an additional 32 low-significance fraction bits. Within the fraction, bits increase in significance from 48 to 63, 32 to 47, 16 to 31, and 0 to 6. The exponent conventions and approximate range of values are the same for both D_floating and F_floating numbers. The precision of a D_floating number is approximately one part in 255 (approximately 16 decimal digits).
Figure 18-6 Double-Precision Real Number Format
In Alpha BASIC, it is possible to lose three binary digits of precision in arithmetic operations when performing operations on D-Float double-precision floating-point data. For each arithmetic operation, the data is converted to G-floating first, the operation is performed in G_floating, and the result is converted back to D-floating when the operation is complete.
Because most floating point values cannot be represented exactly in binary, they are susceptible to rounding. Because Alpha BASIC and the Alpha system hardware use G-floating representation in place of the VAX BASIC D-floating representation, the behavior of floating point computations and comparisons can be different from what you expect. |
The G_floating floating-point number format consists of eight contiguous bytes, starting on an arbitrary byte boundary. Bits are labeled from the right, 0 to 63. The form of a G_floating number is sign magnitude with bit 15 the sign bit, bits 14 to 4 an excess-1024 binary exponent, and bits 3 to 0 and 63 to 16 a normalized 53-bit fraction with the redundant most significant fraction bit not represented.
Within the fraction, bits increase in significance from 48 to 63, 32 to 47, 16 to 31, and 0 to 3. The 11-bit exponent field encodes the values 0 to 2047.
An exponent value of 0 together with a sign bit of 0 indicates that the G_floating number value is 0. Exponent values from 1 to 2047 indicate true binary exponents from -1023 to 1023. The value of a G_floating number is in the approximate range .56 * 10-308 to .9 * 10308; the precision is approximately one part in 252 (approximately 15 decimal digits). Note that both double and G_floating formats require 8 bytes. The G_floating format provides a greater range, but less precision than double-precision format.
18.2.4 HFLOAT Floating-Point Number Format (H_floating)---VAX BASIC Only
In VAX BASIC, an H_floating floating-point number is 16 contiguous
bytes, starting on an arbitrary byte boundary. The H_floating format
combines a large range with extensive precision but requires twice the
amount of storage of double and G_floating numbers. The bits are
labeled from the right, 0 to 127. The form of an H_floating number is
sign magnitude with bit 15 the sign bit, bits 14 to 0 an excess -16384
binary exponent, and bits 127 to 16 a normalized 113-bit fraction with
the redundant most significant fraction bit not represented.
Within the fraction, bits increase in significance from 112 to 127, 96 to 111, 80 to 95, 64 to 79, 48 to 63, 32 to 47, and 16 to 31. The 15-bit exponent field encodes the values 0 through 32767.
An exponent value of 0 together with a sign bit of 0 indicates the
H_floating number has a value of 0. Exponent values from 1 to 32767
indicate true binary exponents from -16383 to 16383. The value of an
H_floating number is in the approximate range .84 * 104932
to .59 * 104932. The precision of an H_floating number is
approximately one part in 2112 (approximately 33 decimal
digits).
18.2.5 SFLOAT Floating-Point Number Format (S_floating)---Alpha BASIC Only
The S_floating floating-point number format consists of four contiguous bytes, starting on an arbitrary byte boundary. Bits are labeled from the right, 0 to 31. The form of an S_floating number is sign magnitude with bit 31 the sign bit, bits 30 to 23 an excess-127 binary exponent, and bits 22 to 0 a normalized 24-bit fraction with the redundant most significant fraction bit not represented unless the exponent is 0. If the exponent is 0, a nonzero fraction represents an unnormalized 23-bit fraction.
An exponent value of 0 together with a fraction value of 0 and a sign
bit of 0 indicates that the S_floating number value is 0. Exponent
values from 1 to 254 indicate true binary exponents from -127 to 127.
The value of an S_floating number is in the approximate range 1.175 *
10-38 to 3.402 * 1038; the precision is
approximately one part in 223 (approximately 7 decimal
digits). Note that S_floating format provides approximately the same
range and precision as F_floating format.
18.2.6 TFLOAT Floating-Point Number Format (T_floating)---Alpha BASIC Only
The T_floating floating-point number format consists of eight contiguous bytes, starting on an arbitrary byte boundary. Bits are labeled from the right, 0 to 63. The form of a T_floating number is sign magnitude with bit 63 the sign bit, bits 62 to 52 an excess-1023 binary exponent, and bits 51 to 0 a normalized 53-bit fraction with the redundant most significant fraction bit not represented unless the exponent is 0. If the exponent is 0, a nonzero fraction represents an unnormalized 52-bit fraction.
An exponent value of 0 together with a fraction value of 0 and a sign
bit of 0 indicates that the T_floating number value is 0. Exponent
values from 1 to 2046 indicate true binary exponents from -1023 to
1023. The value of a T_floating number is in the approximate range
2.225 * 10-308 to 1.797 * 10308; the precision is
approximately one part in 252 (approximately 15 decimal
digits). Note that T_floating format provides approximately the same
range and precision as G_floating format.
18.2.7 XFLOAT Floating-Point Number Format (X_floating)---Alpha BASIC Only
The X_floating floating-point number format consists of sixteen contiguous bytes, starting on an arbitrary byte boundary. Bits are labeled from the right, 0 to 127. The form of an X_floating number is sign magnitude with bit 127 the sign bit, bits 126 to 112 an excess-16383 binary exponent, and bits 111 to 0 a normalized 113-bit fraction with the redundant most significant fraction bit not represented unless the exponent is 0. If the exponent is 0, a nonzero fraction represents an unnormalized 112-bit fraction.
An exponent value of 0 together with a fraction value of 0 and a sign
bit of 0 indicates that the X_floating number value is 0. Exponent
values from 1 to 32766 indicate true binary exponents from -16383 to
16383. The value of an X_floating number is in the approximate range
3.362 * 10-4932 to 1.189 * 104932; the precision
is approximately one part in 2112 (approximately 33 decimal
digits). Note that X_floating format provides approximately the same
range and precision as H_floating format.
18.3 Packed Decimal Number Format
The DECIMAL data type is useful for storing numbers with a fixed decimal point. DECIMAL numbers are stored as a precise representation of the value stored within the constraints of the specified number of fractional digits. A packed decimal string is a contiguous sequence of bytes in memory. The address A and length L are sufficient to specify a packed decimal string, but note that L is the number of digits, not bytes, in the string. Each byte of a packed decimal string is divided into two 4-bit fields (nibbles), each of which must contain decimal digits, except the low nibble of the last byte, which must contain a sign. The representation for the digits or signs is shown in the following table:
| Digit or Sign | Decimal | Hexadecimal |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 1 | 1 |
| 2 | 2 | 2 |
| 3 | 3 | 3 |
| 4 | 4 | 4 |
| 5 | 5 | 5 |
| 6 | 6 | 6 |
| 7 | 7 | 7 |
| 8 | 8 | 8 |
| 9 | 9 | 9 |
| + | 10,12,14, or 15 | A,C,E, or F |
| -- | 11 or 13 | B or D |
Despite the options, the preferred sign representation is 12 for positive and 13 for negative. The length L is the number of digits in the packed decimal string (not counting the sign) and must be in the range 1 to 31. If the number of digits is odd, the digits and the sign fit into ((L/2) + 1) bytes; when the number of digits is even, an extra 0 digit must appear in the high nibble (bits 7 to 4) of the first byte.
The address A of the string specifies the byte of the string containing the most significant digit in its high nibble. Digits of decreasing significance are assigned to increasing byte addresses and from high nibble to low nibble within a byte.
Note that the decimal point is specified by the descriptor for the packed decimal string. See Section 18.6 for more information about packed decimal string descriptions.
| Previous | Next | Contents | Index |