| United States |
|
| Previous | Contents | Index |
The <curses.h> header file defines variables and constants useful for implementing Curses (see Table 6-2).
| Name | Type | Description |
|---|---|---|
| curscr | WINDOW * | Window of current screen |
| stdscr | WINDOW * | Default window |
| LINES | int | Number of lines on the terminal screen |
| COLS | int | Number of columns on the terminal screen |
| ERR | --- | Flag (0) for failed routines |
| OK | --- | Flag (1) for successful routines |
| TRUE | --- | Boolean true flag (1) |
| FALSE | --- | Boolean false flag (0) |
| _BLINK | --- | Parameter for setattr and clrattr |
| _BOLD | --- | Parameter for setattr and clrattr |
| _REVERSE | --- | Parameter for setattr and clrattr |
| _UNDERLINE | --- | Parameter for setattr and clrattr |
For example, you can use the predefined macro ERR to test the success or failure of a Curses function. Example 6-4 shows how to perform such a test.
| Example 6-4 Curses Predefined Variables |
|---|
#include <curses.h>
WINDOW *win1, *win2, *win3;
main()
{
initscr();
win1 = newwin(10, 10, 1, 5);
.
.
.
if (mvwin(win1, 1, 10) == ERR)
addstr("The MVWIN function failed.");
.
.
.
endwin();
}
|
In Example 6-4, if the
mvwin
function fails, the program adds a string to
stdscr
that explains the outcome. The Curses
mvwin
function moves the starting position of a window.
6.6 Cursor Movement
In the UNIX system environment, you can use Curses functions to move the cursor across the terminal screen. With other implementations, you can either allow Curses to move the cursor using the move function, or you can specify the origin and the destination of the cursor to the mvcur function, which moves the cursor in a more efficient manner.
In Compaq C for OpenVMS Systems, the two functions are functionally equivalent and move the cursor with the same efficiency.
Example 6-5 shows how to use the move and mvcur functions.
| Example 6-5 The Cursor Movement Functions |
|---|
#include <curses.h>
main()
{
initscr();
.
.
.
(1) clear();
(2) move(10, 10);
(3) move(LINES/2, COLS/2);
(4) mvcur(0, COLS-1, LINES-1, 0);
.
.
.
endwin();
}
|
Key to Example 6-5:
The following program example shows the effects of many of the Curses macros and functions. You can find explanations of the individual lines of code, if not self-explanatory, in the comments to the right of the particular line. Detailed discussions of the functions follow the source code listing.
Example 6-6 shows the definition and manipulation of one user-defined window and stdscr .
| Example 6-6 stdscr and Occluding Windows |
|---|
/* CHAP_6_STDSCR_OCCLUDE.C */
/* This program defines one window: win1. win1 is */
/* located towards the center of the default window */
/* stdscr. When writing to an occluding window (win1) */
/* that is later erased, the writing is erased as well. */
#include <curses.h> /* Include header file. */
WINDOW *win1; /* Define windows. */
main()
{
char str[80]; /* Variable declaration.*/
initscr(); /* Set up Curses. */
noecho(); /* Turn off echo. */
/* Create window. */
win1 = newwin(10, 20, 10, 10);
box(stdscr, '|', '-'); /* Draw a box around stdscr. */
box(win1, '|', '-'); /* Draw a box around win1. */
refresh(); /* Display stdscr on screen. */
wrefresh(win1); /* Display win1 on screen. */
(1) getstr(str); /* Pause. Type a few words! */
mvaddstr(22, 1, str);
(2) getch();
/* Add string to win1. */
mvwaddstr(win1, 5, 5, "Hello");
wrefresh(win1); /* Add win1 to terminal scr. */
getch(); /* Pause. Press Return. */
delwin(win1); /* Delete win1. */
(3) touchwin(stdscr); /* Refresh all of stdscr. */
getch(); /* Pause. Press Return. */
endwin(); /* Ends session. */
}
|
Key to Example 6-6:
Figure 6-4 An Example of the getch Macro
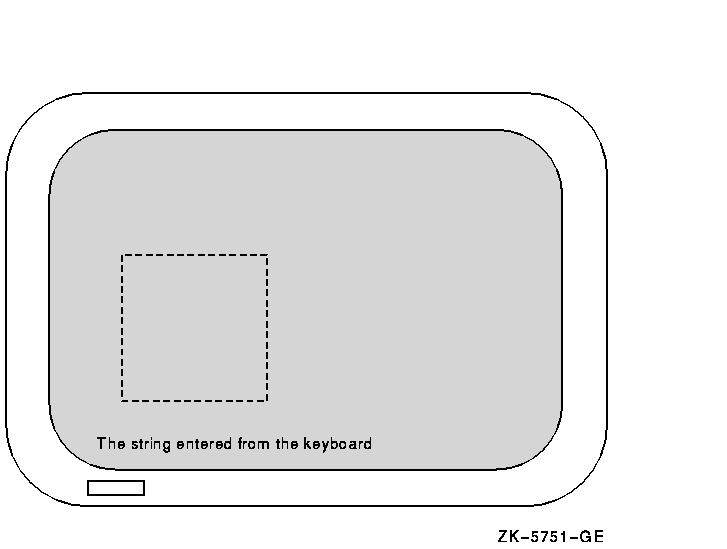
Table 7-1 lists and describes the math functions in the Compaq C Run-Time Library (RTL). For more detailed information on each function, see the Reference Section.
| Function | Description |
|---|---|
| abs | Returns the absolute value of an integer. |
| acos | Returns a value in the range 0 to Pi sign, which is the arc cosine of its radian argument. |
| asin | Returns a value in the range --Pi sign/2 to Pi sign/2, which is the arc sine of its radian argument. |
| atan | Returns a value in the range - pi /2 to Pi sign/2, which is the arc tangent of its radian argument. |
| atan2 | Returns a value in the range - pi to Pi sign, which is the arc tangent of y/x where y and x are the two arguments. |
| cabs | Returns: sqrt ( x * x + y * y ). |
| ceil | Returns (as a double ) the smallest integer that is greater than or equal to its argument. |
| cos | Returns the cosine of its radian argument. |
| cot | Returns the cotangent of its radian argument. |
| cosh | Returns the hyperbolic cosine of its argument. |
| drand48 , erand48 , jrand48 , lrand48 , mrand48 , nrand48 | Generates uniformly distributed pseudorandom number sequences. Returns 48-bit, nonnegative, double-precision floating-point values. |
| exp | Returns the base e raised to the power of the argument. |
| fabs | Returns the absolute value of a floating-point value. |
| floor | Returns (as a double ) the largest integer that is less than or equal to its argument. |
| fmod | Computes the floating-point remainder of the first argument to fmod divided by the second. |
| frexp | Calculates the fractional and exponent parts of a double value. |
| hypot | Returns the square root of the sum of the squares of two arguments. |
| initstate | Initializes random number generators. |
| labs | Returns the absolute value of an integer as a long int . |
| lcong48 | Initializes a 48-bit uniformly distributed pseudorandom number sequence. |
| llabs, qabs (ALPHA ONLY) | Returns the absolute value of an __int64 integer. |
| ldexp | Returns its first argument multiplied by 2 raised to the power of its second argument. |
| ldiv, div | Returns the quotient and remainder after the division of their arguments. |
| lldiv, qdiv (ALPHA ONLY) | Returns the quotient and remainder after the division of their arguments. |
| log, log 10 | Returns the logarithm of their arguments. |
| modf | Returns the positive fractional part of its first argument and assigns the integral part, expressed as a double , to the object whose address is specified by the second argument. |
| pow | Returns the first argument raised to the power of the second argument. |
| rand, srand | Returns pseudorandom numbers in the range 0 to 2 31-1 . |
| random , srandom | Generates pseudorandom numbers in a more random sequence. |
| seed48 , srand48 | Initializes a 48-bit random number generator. |
| setstate | Restarts, and changes random number generators. |
| sin | Returns the sine of its radian argument. |
| sinh | Returns the hyperbolic sine of its argument. |
| sqrt | Returns the square root of its argument. |
| tan | Returns a double value that is the tangent of its radian argument. |
| tanh | Returns a double value that is the hyperbolic tangent of its double argument. |
The following additional Compaq C RTL math routines are supported for Compaq C on OpenVMS Alpha systems only. They are defined in <math.h> . Many of them are float , double , and long double variants of the routines listed in the preceding table. See the Compaq Portable Mathematics Library (DPML) manual for descriptions of these routines.
Note that for programs compiled without /L_DOUBLE=64 (that is, compiled with the default /L_DOUBLE=128), the long double variants of these Compaq C RTL math routines map to the X_FLOAT entry points documented in the DPML manual.
acosd cbrt expm1l ldexpl scalbf
acosdf cbrtf fabsf lgamma scalbl
acosdl cbrtl fabsl lgammaf sind
acosf ceilf fabsl lgammal sindf
acosl ceill finite log10f sindl
acosh copysign finitef log10l sinf
acoshf copysignf finitel log1p sinl
acoshl copysignl floorf log1pf sinhf
asind cosd floorl log1pl sinhl
asindf cosdf fmodf log2 sqrtf
asindl cosdl fmodl log2f sqrtl
asinf cosf fp_class log2l tand
asinl cosl fp_classf logb tandf
asinh coshf fp_classl logbf tandl
asinhf coshl frexpf logbl tanf
asinhl cot frexpl logf tanl
atan2f cotd hypotf logl tanhf
atan2l cotdf hypotl modff tanhl
atand cotdl isnan modfl trunc
atand2 cotf isnanf nextafter truncf
atand2f cotl isnanl nextafterf truncl
atand2l erf j0 nextafterl unordered
atandf erfc j0f nint unorderedf
atandl erfcf j0l nintf unorderedl
atanf erfcl j1 nintl y0
atanl erff j1f powf y0f
atanh erfl j1l powl y0l
atanhf expf jn rint y1
atanhl expl jnf rintf y1f
cabsf expm1 jnl rintl y1l
cabsl expm1f ldexpf scalb yn
ynf
ynl
|
To help you detect run-time errors, the <errno.h> header file defines the following two symbolic values that are returned by many (but not all) of the mathematical functions:
When using the math functions, you can check the external variable errno for either or both of these values and take the appropriate action if an error occurs.
The following program example checks the variable errno for the value EDOM, which indicates that a negative number was specified as input to the function sqrt :
#include <errno.h>
#include <math.h>
#include <stdio.h>
main()
{
double input, square_root;
printf("Enter a number: ");
scanf("%le", &input);
errno = 0;
square_root = sqrt(input);
if (errno == EDOM)
perror("Input was negative");
else
printf("Square root of %e = %e\n",
input, square_root);
}
|
If you did not check
errno
for this symbolic value, the
sqrt
function returns 0 when a negative number is entered. For more
information about the
<errno.h>
header file, see Chapter 4.
7.3 The <fp.h> Header File
The <fp.h> header file implements some of the features defined by the Numerical C Extensions Group of the ANSI X3J11 committee. You might find this useful for applications that make extensive use of floating-point functions.
Some of the double-precision functions listed in this chapter return the value ±HUGE_VAL (defined in either <math.h> or <fp.h> ) if the result is out of range. The float version of those functions return the value HUGE_VALF (defined only in <fp.h> ) for the same conditions. The long double version returns the value HUGE_VALL (also defined in <fp.h> ).
For programs compiled to enable IEEE infinity and NaN values, the values HUGE_VAL, HUGE_VALF, and HUGE_VALL are expressions, not compile-time constants. Initializations such as the following cause a compile-time error:
$ CREATE IEEE_INFINITY.C #include <fp.h> double my_huge_val = HUGE_VAL ^Z $ CC /FLOAT=IEEE/IEEE=DENORM IEEE_INFINITY double my_huge_val = HUGE_VAL; .....................^ %CC-E-NEEDCONSTEXPR, In the initializer for my_huge_val, "decc$gt_dbl_infinity" is not constant, but occurs in a context that requires a constant expression. at line number 3 in file WORK1$:[RTL]IEEE_INFINITY.C;1 $ |
When using both
<math.h>
and
<fp.h>
, be aware that
<math.h>
defines a function
isnan
and
<fp.h>
defines a macro by the same name. Whichever header is included first in
the application will resolve a reference to
isnan
.
7.4 Example
Example 7-1 shows how the tan , sin , and cos functions operate.
| Example 7-1 Calculating and Verifying a Tangent Value |
|---|
/* CHAP_7_MATH_EXAMPLE.C */
/* This example uses two functions --- mytan and main --- */
/* to calculate the tangent value of a number, and to check */
/* the calculation using the sin and cos functions. */
#include <math.h>
#include <stdio.h>
/* This function calculates the tangent using the sin and */
/* cos functions. */
double mytan(x)
double x;
{
double y,
y1,
y2;
y1 = sin(x);
y2 = cos(x);
if (y2 == 0)
y = 0;
else
y = y1 / y2;
return y;
}
main()
{
double x;
/* Print values: compare */
for (x = 0.0; x < 1.5; x += 0.1)
printf("tan of %4.1f = %6.2f\t%6.2f\n", x, mytan(x), tan(x));
}
|
Example 7-1 produces the following output:
$ RUN EXAMPLE tan of 0.0 = 0.00 0.00 tan of 0.1 = 0.10 0.10 tan of 0.2 = 0.20 0.20 tan of 0.3 = 0.31 0.31 tan of 0.4 = 0.42 0.42 tan of 0.5 = 0.55 0.55 tan of 0.6 = 0.68 0.68 tan of 0.7 = 0.84 0.84 tan of 0.8 = 1.03 1.03 tan of 0.9 = 1.26 1.26 tan of 1.0 = 1.56 1.56 tan of 1.1 = 1.96 1.96 tan of 1.2 = 2.57 2.57 tan of 1.3 = 3.60 3.60 tan of 1.4 = 5.80 5.80 $ |
| Previous | Next | Contents | Index |
|
|