HP OpenVMS Systems Documentation

HP Fortran for OpenVMS
User Manual

Intrinsic REAL (KIND=8) or REAL*8 (same as DOUBLE PRECISION) G_float data occupies eight contiguous bytes. The bits are labeled from the right, 0 through 63, as shown in Figure 8-9.

Figure 8-9 VAX G_float REAL (KIND =8) or REAL*8 Representation

The form of REAL (KIND=8) or REAL*8 G_float data is sign magnitude, where:

• Bit 15 is the sign bit (0 for positive numbers, 1 for negative numbers).
• Bits 14:4 are a binary exponent in excess 1024 notation (binary exponents from --1023 to 1023 are represented by the binary 1 to 2047).
• Bits 3:0 and 63:16 are a normalized 53-bit fraction with the redundant most significant fraction bit not represented.

The value of data is in the approximate range: 0.5562684646268004D--308 to 0.89884656743115785407D308.

The precision of G_float data is approximately one part in 2**52, typically 15 decimal digits.

8.4.3.3 VAX D_float Representation

Intrinsic REAL (KIND=8) or REAL*8 (same as DOUBLE PRECISION) D_float data occupies eight contiguous bytes. Bits are labeled from the right, 0 through 63, as shown in Figure 8-10.

Figure 8-10 VAX D_float REAL (KIND =8) or REAL*8 Representation

The form of REAL (KIND=8) or REAL*8 D_float data is identical to an F_float real number, except for an additional 32 low-significance fraction bits. The exponent conventions and approximate range of values are the similar to those for F_float.

The value of data is in the approximate range: 0.2938735877055719D--38 to 1.70141183460469229D38.

The precision is approximately one part in 2**55, typically 16 decimal digits. Calculations with D_float data on Alpha systems use G_float precision (53-bit instead of 56-bit fraction).

For information about how D_float and G_float calculations are done on I64 systems, see Appendix A.

8.4.4 REAL (KIND=16) or REAL*16 X_float Representation

REAL*16 data occupies 16 contiguous bytes stored in X_float format. Bits are labeled from the right, 0 through 127, as shown in Figure 8-11.

Figure 8-11 X_float REAL (KIND =16) Floating-Point Data Representation

The form of REAL (KIND=16) data is sign magnitude, with:

• Bit 127 the sign bit (0 for positive numbers, 1 for negative numbers)
• Bits 126:112 a binary exponent in excess 16383 notation
• Bits 111:0 a normalized 113-bit fraction including the redundant most-significant fraction bit not represented.

The value of data is in the approximate range: 6.4751751194380251109244389582276465524996Q-4966 to 1.189731495357231765085759326628007016196477Q4932. The smallest normalized number is 3.362103143112093506262677817321753Q-4932.

In contrast to other floating-point formats, there is little if any performance penalty from using denormalized extended-precision numbers. This is because accessing denormalized REAL (KIND=16) numbers does not result in an arithmetic trap (the extended-precision format is emulated in software).

The precision is approximately one part in 2**112 or typically 33 decimal digits.

8.4.5 COMPLEX (KIND=4) or COMPLEX*8 Representations

COMPLEX (KIND=4) or COMPLEX*4 data can be in IEEE S_float or VAX F_float formats. This is the default data size for COMPLEX declarations.

Intrinsic COMPLEX (KIND=4) or COMPLEX*8 (single-precision COMPLEX) data is eight contiguous bytes containing a pair of REAL (KIND=4) or REAL*4 values stored in IEEE S_float format or VAX F_float format.

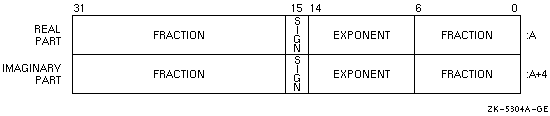
The low-order four bytes contain REAL (KIND=4) data that represents the real part of the complex number. The high-order four bytes contain REAL (KIND=4) data that represents the imaginary part of the complex number,

The limits (and underflow characteristics for S_float numbers) for REAL (KIND=4) or REAL*4 apply to the two separate real and imaginary parts of a COMPLEX (KIND=4) or COMPLEX*8 number. Like REAL (KIND=4) numbers, the sign bit representation is 0 (zero) for positive numbers and 1 for negative numbers.

Figure 8-12 shows the IEEE S_float representation of COMPLEX (KIND=4) or COMPLEX*8 numbers.

Figure 8-12 IEEE S_float COMPLEX (KIND =4) or COMPLEX*8 Representation

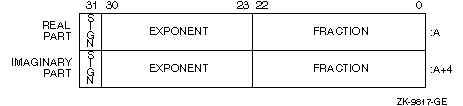
Figure 8-13 shows the VAX F_float representation of COMPLEX (KIND=4) or COMPLEX*8 numbers.

Figure 8-13 VAX F_float COMPLEX (KIND =4) or COMPLEX*8 Representation

COMPLEX (KIND=8) or COMPLEX*16 data can be in IEEE T_float, VAX G_float, or VAX D_float formats.

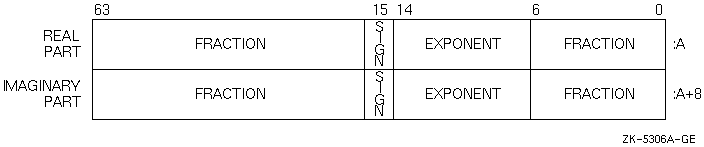
Intrinsic COMPLEX (KIND=8) or COMPLEX*16 (same as DOUBLE COMPLEX) data is 16 contiguous bytes containing a pair of REAL*8 values stored in IEEE T_float format, VAX G_float, or VAX D_float formats.

The low-order eight bytes contain REAL (KIND=8) data that represents the real part of the complex data. The high-order eight bytes contain REAL (KIND=8) data that represents the imaginary part of the complex data.

Like REAL (KIND=8) or REAL*8 numbers, the sign bit representation is 0 (zero) for positive numbers and 1 for negative numbers. The limits (and underflow characteristics for T_float numbers) apply to the two separate real and imaginary parts of a COMPLEX (KIND=8) or COMPLEX*16 number.

Figure 8-14 shows the IEEE T_float COMPLEX (KIND=8) or COMPLEX*16 representation.

Figure 8-14 IEEE T_float COMPLEX (KIND =8) or COMPLEX*16 Representation

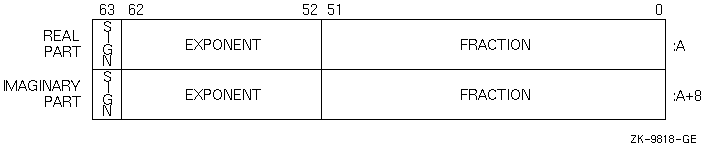
Figure 8-15 (G_float) and Figure 8-16 (D_float) show the representation of the VAX COMPLEX (KIND=8) or COMPLEX*16 numbers.

Figure 8-15 VAX G_float COMPLEX (KIND =8) or COMPLEX*16 Representation

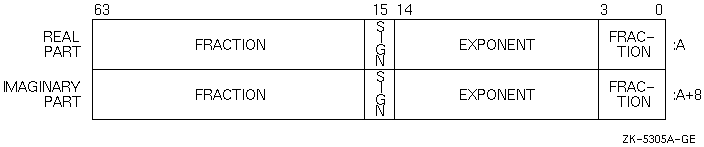
Figure 8-16 VAX D_float COMPLEX (KIND =8) or COMPLEX*16 Representation

Intrinsic COMPLEX (KIND=16) or COMPLEX*32 (extended precision) data is 32 contiguous bytes containing a pair of REAL*16 values stored in IEEE-style X_float.

The low-order 16 bytes contain REAL (KIND=16) data that represents the real part of the complex data. The high-order 16 bytes contain REAL (KIND=16) data that represents the imaginary part of the complex data, as shown in Figure 8-17.

Figure 8-17 COMPLEX (KIND =16) or COMPLEX*32 Representation

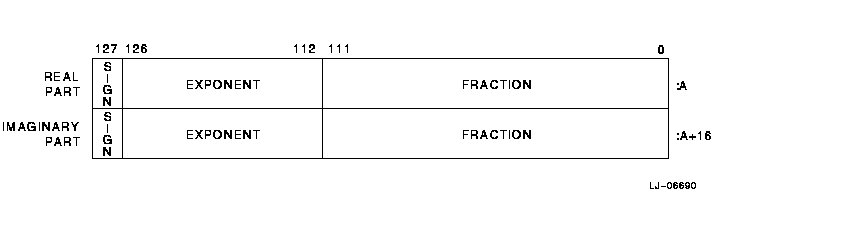
The limits and underflow characteristics for REAL (KIND=16) apply to the two separate real and imaginary parts of a COMPLEX (KIND=16) or COMPLEX*32 number. Like REAL (KIND=16) numbers, the sign bit representation is 0 (zero) for positive numbers and 1 for negative numbers.

For More Information:

• On converting unformatted data, see Chapter 9.
• On defining constants and assigning values to variables, see the HP Fortran for OpenVMS Language Reference Manual.
• On intrinsic functions related to the various data types, such as SELECTED_REAL_KIND, see the HP Fortran for OpenVMS Language Reference Manual.
• On OpenVMS VAX floating-point data types (provided for those converting OpenVMS data), see Section B.8.
• On the FORTRAN command qualifiers that control the size of REAL and COMPLEX declarations (without a kind parameter or size specifier), see Section 2.3.37.
• On the FORTRAN command qualifiers that control the size of DOUBLE PRECISION declarations, see Section 2.3.17.
• On IEEE binary floating-point, see the IEEE Standard for Binary Floating-Point Arithmetic (ANSI/IEEE Standard 754-1985).

Exceptional values usually result from a computation and include plus infinity, minus infinity, NaN, and denormalized numbers. Exceptional values and the representation of zero are associated only with IEEE S_float, T_float, and X_float formats (/FLOAT=IEEE_FLOAT qualifier), not with VAX floating-point formats. (VAX floating-point representation of minus (--) zero causes a reserved operand fault on VAX systems.)

Floating-point numbers can be one of the following:

• Finite number---A floating-point number that represents a valid number (bit pattern) within the normalized ranges of a particular data type, including --max to --min,---zero, +zero, +min to +max.
  For any native floating-point data type, the values of min or max are listed in Section 8.4.2 (single precision), Section 8.4.3 (double precision), and Section 8.4.4 (extended precision).
  For native VAX floating-point data types, finite numbers do not include reserved operand or dirty zero values.
  Special bit patterns that are not finite numbers represent exceptional values.
• Infinity---An IEEE floating-point bit pattern that represents plus or minus infinity. HP Fortran identifies infinity values with the letters "Infinity" or asterisks (******) in output statements (depends on field width) or certain hexadecimal values (fraction of 0 and exponent of all 1 values).
• Not-a-Number (NaN)---An IEEE floating-point bit pattern that represents something other than a number. HP Fortran identifies NaN values with the letters "NaN" in output statements. A NaN can be a signaling NaN or a quiet NaN:
  • A quiet NaN might occur as a result of a calculation, such as 0./0. It has an exponent of all 1 values and initial fraction bit of 1.
  • A signaling NaN must be set intentionally (does not result from calculations) and has an exponent of all 1 values and initial fraction bit of 0 (with one or more other fraction bits of 1).
• Denormal---Identifies an IEEE floating-point bit pattern that represents a number whose value falls between zero and the smallest finite (normalized) number for that data type. The exponent field contains all zeros.
  For negative numbers, denormalized numbers range from the next representable value larger than minus zero to the representable value that is one bit less than the smallest finite (normalized) negative number. For positive numbers, denormalized numbers range from the next representable value larger than positive zero to the representable value that is one bit less than the smallest finite (normalized) positive number.
• Zero---Can be the value +0 (all zero bits, also called true zero) or -0 (all zero bits except the sign bit, such as Z ' 8000000000000000 ' ).

A NaN or infinity value might result from a calculation that contains a divide by zero, overflow, or invalid data.

A denormalized number occurs when the result of a calculation falls within the denormalized range for that data type (subnormal value).

To control floating-point exception handling at run time for the main program, use the appropriate /IEEE_MODE qualifier keyword. For example, if an exceptional value is used in a calculation, an unrecoverable exception can occur unless you specify the appropriate /IEEE_MODE qualifier keyword. Denormalized numbers can be processed as is, set equal to zero with program continuation or a program stop, and generate warning messages (see Section 2.3.24).

Table 8-2 lists the hexadecimal (hex) values of the IEEE exceptional floating-point numbers for S_float (single precision), T_float (double precision), and X_float (extended precision) formats:

HP Fortran supports IEEE exception handling, allowing you to test for infinity by using a comparison of floating-point data (such as generating positive infinity by using a calculation such as x=1.0/0 and comparing x to the calculated number).

The appropriate FORTRAN command /IEEE_MODE qualifier keyword allows program continuation when a calculation results in a divide by zero, overflow, or invalid data arithmetic exception, generating an exceptional value (a NaN or Infinity (+ or --)).

To test for a NaN when HP Fortran allows continuation for arithmetic exception, you can use the ISNAN intrinsic function. Example 8-1 shows how to use the ISNAN intrinsic function to test whether a REAL*8 (DOUBLE PRECISION) value contains a NaN.

      DOUBLE PRECISION A, B, F
      A = 0.
      B = 0.

!     Perform calculations with variables A and B
      .
      .
      .

!     f contains the value to check against a particular NaN

      F = A / B

      IF (ISNAN(F)) THEN
        WRITE (6,*) '--> Variable F contains a NaN value <--'
      ENDIF

!     Inform user that f has the hardware quiet NaN value
!     Perform calculations with variable F (or stop program early)

      END

To allow continuation when a NaN (or other exceptional value) is encountered in a calculation, this program might be compiled with /FLOAT=IEEE_FLOAT and /IEEE_MODE=UNDERFLOW_TO_ZERO (or /IEEE_MODE=DENORM_RESULTS) qualifiers:

$ FORTRAN/FLOAT=IEEE_FLOAT/IEEE_MODE=UNDERFLOW_TO_ZERO ISNAN
$ LINK ISNAN
$ RUN ISNAN
--> Variable F contains a NaN value <--

To enable additional run-time message reporting with traceback information (source line correlation), use the FORTRAN command qualifier /CHECK=FP_EXCEPTIONS.

The FP_CLASS intrinsic function is also available to check for exceptional values (see the HP Fortran for OpenVMS Language Reference Manual).

For More Information:

• On using the FORTRAN command /IEEE_MODE qualifier keywords to control arithmetic exception handling, see Section 2.3.24.
• On floating-point architecture, see the Intel Itanium Architecture Software Developer's Manual, Volume 1: Application Architecture.
• On Alpha exceptional values, see the Alpha Architecture Reference Manual.
• On IEEE binary floating-point exception handling, see the IEEE Standard for Binary Floating-Point Arithmetic (ANSI/IEEE Standard 754-1985).

A character string is a contiguous sequence of bytes in memory, as shown in Figure 8-18.

Figure 8-18 CHARACTER Data Representation

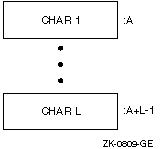
A character string is specified by two attributes: the address A of the first byte of the string, and the length L of the string in bytes. The length L of a string is in the range 1 through 65,535.

For More Information:

• On defining constants and assigning values to variables, using substring expressions and concatenation, see the HP Fortran for OpenVMS Language Reference Manual.
• On intrinsic functions related to the various data types, see the HP Fortran for OpenVMS Language Reference Manual.

Hollerith constants are stored internally, one character per byte. When Hollerith constants contain the ASCII representation of characters, they resemble the storage of character data (see Figure 8-18).

When Hollerith constants store numeric data, they usually have a length of one, two, four, or eight bytes and resemble the corresponding numeric data type.

For More Information:

• On defining constants and assigning values to variables, see the HP Fortran for OpenVMS Language Reference Manual.
• On intrinsic functions related to the various data types, see the HP Fortran for OpenVMS Language Reference Manual.