| Previous | Contents | Index |
For More Information:
A whole array is a named array; it is either a named constant or a variable. It is referenced by using the array name (without any subscripts).
If a whole array appears in a nonexecutable statement, the statement applies to the entire array. For example:
INTEGER, DIMENSION(2:11,3) :: L ! Specifies the type and
! dimensions of array L
|
If a whole array appears in an executable statement, the statement applies to all of the elements in the array. For example:
L = 10 ! The value 10 is assigned to all the
! elements in array L
WRITE *, L ! Prints all the elements in array L
|
An array element is one of the scalar data items that make up an array. A subscript list (appended to the array or array component) determines which element is being referred to. A reference to an array element takes the following form:
|
array(subscript-list) |
array
Is the name of the array.subscript-list
Is a list of one or more subscripts separated by commas. The number of subscripts must equal the rank of the array.Each subscript must be a scalar integer (or other numeric) expression with a value that is within the bounds of its dimension.
Each array element inherits the type, kind type parameter, and certain attributes (INTENT, PARAMETER, and TARGET) of the parent array. An array element cannot inherit the POINTER attribute.
If an array element is of type character, it can be followed by a substring range in parentheses; for example:
ARRAY_D(1,2) (1:3) ! Elements are substrings of length 3 |
However, by convention, such an object is considered to be a substring rather than an array element.
The following are some valid array element references for an array declared as REAL B(10,20): B(1,3), B(10,10), and B(5,8).
For information on forms for array specifications, see Section 5.1.4.
The elements of an array form a sequence known as array element order. The position of an element in this sequence is its subscript order value.
The elements of an array are stored as a linear sequence of values. A one-dimensional array is stored with its first element in the first storage location and its last element in the last storage location of the sequence. A multidimensional array is stored so that the leftmost subscripts vary most rapidly. This is called the order of subscript progression.
Figure 3-1 shows array storage in one, two, and three dimensions.
Figure 3-1 Array Storage
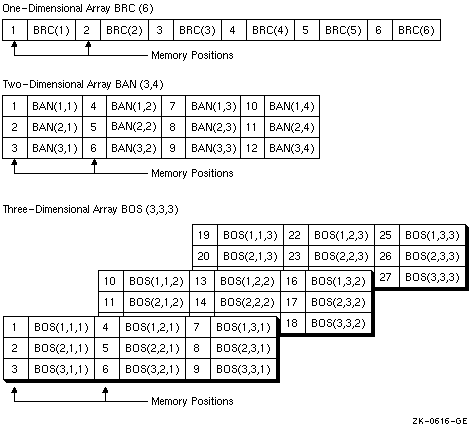
For example, in two-dimensional array BAN, element BAN(1,2) has a subscript order value of 4; in three-dimensional array BOS, element BOS(1,1,1) has a subscript order value of 1.
In an array section, the subscript order of the elements is their order within the section itself. For example, if an array is declared as B(20), the section B(4:19:4) consists of elements B(4), B(8), B(12), and B(16). The subscript order value of B(4) in the array section is 1; the subscript order value of B(12) in the section is 3.
An array section is a portion of an array that is an array itself. It is an array subobject. A section subscript list (appended to the array or array component) determines which portion is being referred to. A reference to an array section takes the following form:
|
array(sect-subscript-list) |
array
Is the name of the array.sect-subscript-list
Is a list of one or more section subscripts (subscripts, subscript triplets, or vector subscripts) indicating a set of elements along a particular dimension.At least one of the items in the section subscript list must be a subscript triplet or vector subscript. A subscript triplet specifies array elements in increasing or decreasing order at a given stride. A vector subscript specifies elements in any order.
Each subscript and subscript triplet must be a scalar integer (or other numeric) expression. Each vector subscript must be a rank-one integer expression.
If no section subscript list is specified, the rank and shape of the array section is the same as the parent array.
Otherwise, the rank of the array section is the number of vector subscripts and subscript triplets that appear in the list. Its shape is a rank-one array where each element is the number of integer values in the sequence indicated by the corresponding subscript triplet or vector subscript.
If any of these sequences is empty, the array section has a size of zero. The subscript order of the elements of an array section is that of the array object that the array section represents.
Each array section inherits the type, kind type parameter, and certain attributes (INTENT, PARAMETER, and TARGET) of the parent array. An array section cannot inherit the POINTER attribute.
If an array (or array component) is of type character, it can be followed by a substring range in parentheses. Consider the following declaration:
CHARACTER(LEN=15) C(10,10) |
In this case, an array section referenced as C(:,:) (1:3) is an array of shape (10,10), whose elements are substrings of length 3 of the corresponding elements of C.
The following shows valid references to array sections. Note that the syntax (/.../) denotes an array constructor (see Section 3.5.2.4).
REAL, DIMENSION(20) :: B
...
PRINT *, B(2:20:5) ! The section consists of elements
! B(2), B(7), B(12), and B(17)
K = (/3, 1, 4/)
B(K) = 0.0 ! Section B(K) is a rank-one array with shape (3) and
! size 3. (0.0 is assigned to B(1), B(3), and B(4).)
|
A subscript triplet is a set of three values representing the lower bound of the array section, the upper bound of the array section, and the increment (stride) between them. It takes the following form:
|
[first-bound] : [last-bound] [:stride] |
first-bound
Is a scalar integer (or other numeric) expression representing the first value in the subscript sequence. If omitted, the declared lower bound of the dimension is used.last-bound
Is a scalar integer (or other numeric) expression representing the last value in the subscript sequence. If omitted, the declared upper bound of the dimension is used.When indicating sections of an assumed-size array, this subscript must be specified.
stride
Is a scalar integer (or other numeric) expression representing the increment between successive subscripts in the sequence. It must have a nonzero value. If it is omitted, it is assumed to be 1.
The stride has the following effects:
B(2,1,2) B(2,2,2)
B(3,1,2) B(3,2,2)
B(4,1,2) B(4,2,2)
A(10)
A(8)
A(6)
A(4)
If a range specified by the stride is empty, the array section has a size of zero.
A subscript in a subscript triplet need not be within the declared bounds for that dimension if all values used to select the array elements are within the declared bounds. For example, if an array has been declared as A(15), the array section specified as A(4:16:10) is valid. The section is a rank-one array with shape (2) and size 2. It consists of elements A(4) and A(14).
If the subscript triplet does not specify bounds or stride, but only a colon (:), the entire declared range for the dimension is used.
A vector subscript is a one-dimensional (rank one) array of integer values (within the declared bounds for the dimension) that selects a section of a whole (parent) array. The elements in the section do not have to be in order and the section can contain duplicate values.
For example, A is a rank-two array of shape (4,6). B and C are rank-one arrays of shape (2) and (3), respectively, with the following values:
B = (/1,4/) ! Syntax (/.../) denotes an array constructor C = (/2,1,1/) ! This constructor produces a many-one array section |
Array section A(3,B) consists of elements A(3,1) and A(3,4). Array section A(C,1) consists of elements A(2,1), A(1,1), and A(1,1). Array section A(B,C) consists of the following elements:
A(1,2) A(1,1) A(1,1)
A(4,2) A(4,1) A(4,1)
An array section with a vector subscript that has two or more elements with the same value is called a many-one array section. A many-one section must not appear on the left of the equal sign in an assignment statement, or as an input item in a READ statement.
The following assignments to C also show examples of vector subscripts:
INTEGER A(2), B(2), C(2) ... B = (/1,2/) C(B) = A(B) C = A((/1,2/)) |
An array section with a vector subscript must not be any of the following:
If the sequence specified by the vector subscript is empty, the array section has a size of zero.
An array constructor can be used to create and assign values to rank-one arrays (and array constants). An array constructor takes the following form:
|
(/ac-value-list/) |
ac-value-list
Is a list of one or more expressions or implied-do loops. Each ac-value must have the same type and kind parameters, and be separated by commas.
An implied-do loop in an array constructor takes the following form:
|
(ac-value-expr, do-variable = expr1, expr2 [,expr3]) |
ac-value-expr
Is a scalar expression evaluated for each value of the do-variable to produce an array element value.do-variable
Is the name of a scalar integer variable. Its scope is that of the implied-do loop.expr
Is a scalar integer expression. The expr1 and expr2 specify a range of values for the loop; expr3 specifies the stride. The expr3 must be a nonzero value; if it is omitted, it is assumed to be 1.
The array constructed has the same type as the ac-value-list expressions.
If the sequence of values specified by the array constructor is empty (there are no expressions or the implied-do loop produces no values), the rank-one array has a size of zero.
An ac-value is interpreted as follows:
| Form of ac-value | Result |
|---|---|
| A scalar expression | Its value is an element of the new array. |
| An array expression | The values of the elements in the expression (in array element order) are the corresponding sequence of elements in the new array. |
| An implied-do loop | It is expanded to form a list of array elements under control of the DO variable (like a DO construct). |
The following shows the three forms of an ac-value:
C1 = (/4,8,7,6/) ! A scalar expression C2 = (/B(I, 1:5), B(I:J, 7:9)/) ! An array expression C3 = (/(I, I=1, 4)/) ! An implied-do loop |
You can also mix these forms, for example:
C4 = (/4, A(1:5), (I, I=1, 4), 7/) |
If every expression in an array constructor is a constant expression, the array constructor is a constant expression.
If the expressions are of type character, Fortran 95/90 requires each
expression to have the same character length.
However, HP Fortran allows the character expressions to be of
different character lengths. The length of the resultant character
array is the maximum of the lengths of the individual character
expressions. For example:
This causes the following to be displayed:
print *,len ( (/'a','ab','abc','d'/) )
print *,'++'//(/'a','ab','abc','d'/)//'--'
3
++a --++ab --++abc--++d --
If an implied-do loop is contained within another implied-do loop (nested), they cannot have the same DO variable (do-variable).
To define arrays of more than one dimension, use the RESHAPE intrinsic
function.
The following are alternative forms for array constructors:
INTEGER C(4)
C = (/4,8,7,6/)
C = [4,8,7,6]
INTEGER D(3)
D = (/1:5:2/) ! Triplet form
D = (/(I, I=1, 5, 2)/) ! Implied-do loop form
The following example shows an array constructor using an implied-do loop:
INTEGER ARRAY_C(10) ARRAY_C = (/(I, I=30, 48, 2)/) |
The values of ARRAY_C are the even numbers 30 through 48.
The following example shows an array constructor of derived type that uses a structure constructor:
TYPE EMPLOYEE
INTEGER ID
CHARACTER(LEN=30) NAME
END TYPE EMPLOYEE
TYPE(EMPLOYEE) CC_4T(4)
CC_4T = (/EMPLOYEE(2732,"JONES"), EMPLOYEE(0217,"LEE"), &
EMPLOYEE(1889,"RYAN"), EMPLOYEE(4339,"EMERSON")/)
|
The following example shows how the RESHAPE intrinsic function can be used to create a multidimensional array:
E = (/2.3, 4.7, 6.6/) D = RESHAPE(SOURCE = (/3.5, (/2.0, 1.0/), E/), SHAPE = (/2,3/)) |
D is a rank-two array with shape (2,3) containing the following elements:
3.5 1.0 4.7
2.0 2.3 6.6
| Previous | Next | Contents | Index |